无感FOC电机驱动

相关仿真模型地址：ChenZR0509/FOC-: 存放FOC驱动学习过程中用到的资料以及笔记

第一部分 扩展卡尔曼滤波算法

第一章 扩展卡尔曼滤波算法方程组

状态预测方程：x^n+1∣n=x^n∣n+f~nx^n∣n+B~nun状态预测方程：\hat{x}_{n+1|n}=\hat{x}_{n|n}+\widetilde{f}_n\hat{x}_{n|n}+\widetilde{B}_nu_n

协方差预测方程：Pn+1∣n=A~nPn∣nA~nT+Q协方差预测方程：P_{n+1|n}=\widetilde{A}_nP_{n|n}\widetilde{A}_{n}^{T}+Q

观测方程：zn=h(xn)观测方程：z_n=h\left( x_n \right)

状态更新方程：x^n∣n=x^n∣n−1+Kn(zn−h(x^n∣n−1))状态更新方程：\hat{x}_{n|n}=\hat{x}_{n|n-1}+K_n\left( z_n-h\left( \hat{x}_{n|n-1} \right) \right)

协方差更新方程：Pn∣n=(I−KnH~n)Pn∣n−1协方差更新方程：P_{n|n}=\left( I-K_n\widetilde{H}_n \right) P_{n|n-1}

卡尔曼增益方程：Kn=Pn∣n−1H~nT(H~nPn∣n−1H~nT+Rn)−1卡尔曼增益方程：K_n=P_{n|n-1}\widetilde{H}_{n}^{T}\left( \widetilde{H}_nP_{n|n-1}\widetilde{H}_{n}^{T}+R_n \right) ^{-1}

第二章 扩展卡尔曼滤波FOC电机驱动应用

  • 已知永磁同步电机在α轴和β轴下的电压平衡方程为：

    {Uα=Riα+Ldiαdt−weψfsin⁡θeUβ=Riβ+Ldiβdt+weψfcos⁡θe\left\{ \begin{array}{l} U_{\alpha}=Ri_{\alpha}+L\frac{di_{\alpha}}{dt}-w_e\psi _f\sin \theta _e\\ U_{\beta}=Ri_{\beta}+L\frac{di_{\beta}}{dt}+w_e\psi _f\cos \theta _e\\ \end{array} \right.

  • 以电流为状态，故而可得其状态方程为：

    {diαdt=−RLiα+1LUα+1Lweψfsin⁡θediβdt=−RLiβ+1LUβ−1Lweψfcos⁡θe\left\{ \begin{array}{l} \frac{di_{\alpha}}{dt}=-\frac{R}{L}i_{\alpha}+\frac{1}{L}U_{\alpha}+\frac{1}{L}w_e\psi _f\sin \theta _e\\ \frac{di_{\beta}}{dt}=-\frac{R}{L}i_{\beta}+\frac{1}{L}U_{\beta}-\frac{1}{L}w_e\psi _f\cos \theta _e\\ \end{array} \right.

  • 仅考虑匀速转动的情况可得转速和角度方程为：

    {dwedt=0dθedt=we\left\{ \begin{array}{l} \frac{dw_e}{dt}=0\\ \frac{d\theta _e}{dt}=w_e\\ \end{array} \right.

  • 联立可得：

    {diαdt=−RLiα+1LUα+1Lweψfsin⁡θediβdt=−RLiβ+1LUβ−1Lweψfcos⁡θedwedt=0dθedt=we\left\{ \begin{array}{l} \frac{di_{\alpha}}{dt}=-\frac{R}{L}i_{\alpha}+\frac{1}{L}U_{\alpha}+\frac{1}{L}w_e\psi _f\sin \theta _e\\ \frac{di_{\beta}}{dt}=-\frac{R}{L}i_{\beta}+\frac{1}{L}U_{\beta}-\frac{1}{L}w_e\psi _f\cos \theta _e\\ \frac{dw_e}{dt}=0\\ \frac{d\theta _e}{dt}=w_e\\ \end{array} \right.

  • 特取非线性状态空间方程格式为：

    {x˙=f(x)+Buy=Cx+Du\left\{ \begin{array}{l} \dot{x}=f\left( x \right) +Bu\\ y=Cx+Du\\ \end{array} \right.

  • 各变量取值如下所示：

    状态变量：x=[iαiβweθe]状态变量：x=\left[ \begin{array}{c} i_{\alpha}\\ i_{\beta}\\ w_e\\ \theta _e\\ \end{array} \right]

    输入变量：u=[UαUβ]输入变量：u=\left[ \begin{array}{c} U_{\alpha}\\ U_{\beta}\\ \end{array} \right]

    输出变量：y=[iαiβweθe]输出变量：y=\left[ \begin{array}{c} i_{\alpha}\\ i_{\beta}\\ w_e\\ \theta _e\\ \end{array} \right]

  • 测量方程不同于输出方程，我们仅需测量输出信号的前两个元素即可，因此：

    观测方程：zn=h(xn)=Cx+Du=Hx观测方程：z_n=h\left( x_n \right) =Cx+Du=Hx

    测量变量：z=[iαiβ]测量变量：z=\left[ \begin{array}{c} i_{\alpha}\\ i_{\beta}\\ \end{array} \right]

  • 因此可得：

    f~n=ΔT[−RLiα+1Lweψfsin⁡θe−RLiβ−1Lweψfcos⁡θe0we]\widetilde{f}_n=\varDelta T\left[ \begin{array}{c} -\frac{R}{L}i_{\alpha}+\frac{1}{L}w_e\psi _f\sin \theta _e\\ -\frac{R}{L}i_{\beta}-\frac{1}{L}w_e\psi _f\cos \theta _e\\ 0\\ w_e\\ \end{array} \right]

    A~n=[1−RLΔT01Lψfsin⁡θeΔT1Lweψfcos⁡θeΔT01−RLΔT−1Lψfcos⁡θeΔT1Lweψfsin⁡θeΔT00100011]∣xn=x^n∣n\widetilde{A}_n=\left. \left[ \begin{matrix} 1-\frac{R}{L}\varDelta T& 0& \frac{1}{L}\psi _f\sin \theta _e\varDelta T& \frac{1}{L}w_e\psi _f\cos \theta _e\varDelta T\\ 0& 1-\frac{R}{L}\varDelta T& -\frac{1}{L}\psi _f\cos \theta _e\varDelta T& \frac{1}{L}w_e\psi _f\sin \theta _e\varDelta T\\ 0& 0& 1& 0\\ 0& 0& 1& 1\\ \end{matrix} \right] \right|_{_{_{x_n=\hat{x}_{n|n}}}}

    B=[1L001L0000]B=\left[ \begin{matrix} \frac{1}{L}& 0\\ 0& \frac{1}{L}\\ 0& 0\\ 0& 0\\ \end{matrix} \right]

    B~n=BΔT=[1LΔT001LΔT0000]\widetilde{B}_n=B\varDelta T=\left[ \begin{matrix} \frac{1}{L}\varDelta T& 0\\ 0& \frac{1}{L}\varDelta T\\ 0& 0\\ 0& 0\\ \end{matrix} \right]

    C=[1000010000100001]C=\left[ \begin{matrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\\ \end{matrix} \right]

    D=[0000]D=\left[ \begin{array}{c} 0\\ 0\\ 0\\ 0\\ \end{array} \right]

    H=[10000100]H=\left[ \begin{matrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ \end{matrix} \right]

第三章 扩展卡尔曼滤波M文件编写

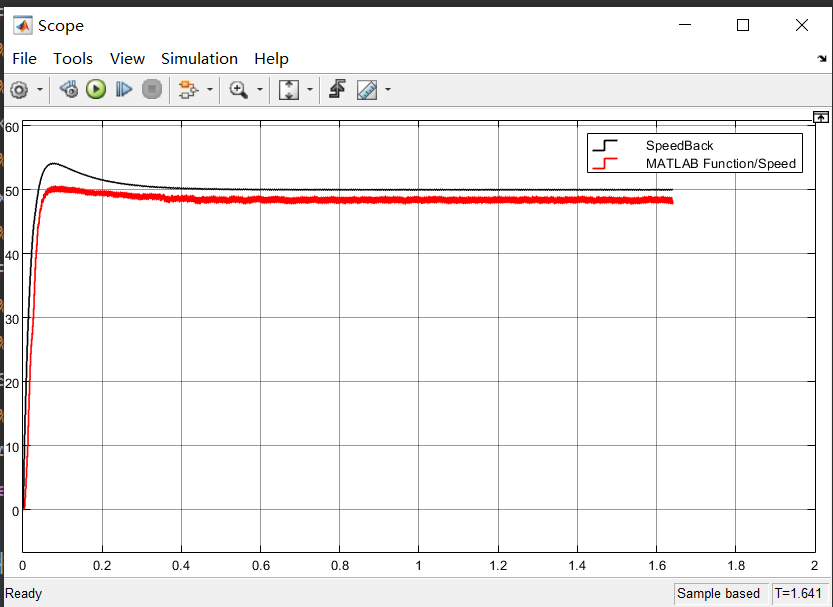
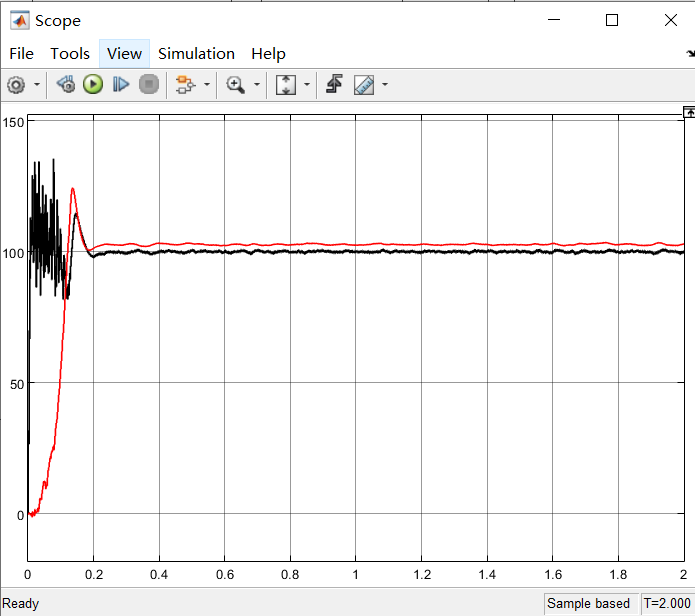
旨在不使用编码器等传感器以预测电机转动角度和速度等信息；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
function [Speed,Angle] = EKF(ualpha,ubeta,ialpha,ibeta,R,L,Flux,Pn)
persistent Flag x Pm;
%1、进行数据初始化
if isempty(Flag)
    Flag = 1;
    %初始化状态向量
    x=zeros(4,1);
    %定义协方差矩阵
    Pm=diag([0 0 0 0]);
end
%2、定义过程噪声协方差矩阵
Qm=[0.001,0,0,0; 0,0.001,0,0; 0,0,0.001,0; 0,0,0,0.001];
%3、定义观测噪声协方差矩阵
Rm=[0.001,0; 0,0.001];
%4、定义相邻两次卡尔曼滤波运行间隔时间
Ts=1e-6;
%5、定义系统矩阵
Am=[-R/L,0,Flux/L*sin(x(4)),Flux/L*x(3)*cos(x(4));
           0,-R/L,-Flux/L*cos(x(4)),Flux/L*x(3)*sin(x(4));
           0,0,1,0;
           0,0,1,1];
%2、定义输入矩阵
Bm=[1.0/L,0; 0,1.0/L; 0,0; 0,0];
%3、定义观测矩阵
Hm=eye(2,4);
%4、定义非线性矩阵
Fm=[-R/L*x(1)+Flux/L*x(3)*sin(x(4));
         -R/L*x(2)-Flux/L*x(3)*cos(x(4));
         0
         x(3)];
%5、离散化模型
AmHat=eye(4)+Ts*Am;
BmHat=Ts*Bm;
FmHat=Ts*Fm;
%6、读取输入变量
u=[ualpha;ubeta];
%7、读取测量变量
z=[ialpha;ibeta];
% ------------ 预测步骤 ------------
%8、状态预测
xHat=x+FmHat+BmHat*u;
%9、测量变量的预测
zHat=Hm*xHat;
%10、协方差预测
PmHat=AmHat*Pm*AmHat'+Qm;
% ------------ 更新步骤 ------------
%11、计算卡尔曼增益
Km=PmHat*Hm'/(Hm*PmHat*Hm'+Rm);
%12、更新状态变量       
x=xHat+Km*(z-zHat);
%13、协方差更新
Pm=(eye(4)-Km*Hm)*PmHat;
%14、电机转速和电转角的输出
%电机的实际转速
Speed=x(3)/Pn;
%电机的电角度
Angle=rem(x(4),2*pi);
end

  • 将其放在有感FOC驱动仿真中滤波器查看实际值和观测值，如下图所示：

    image-20241120135005989

  • 将其放在无感FOC驱动的反馈中，可得：

    image-20241120144310284