卡尔曼滤波
第一部分 数学基础
第一章 概率论回顾
-
均值:即一组真实数据的平均值,其计算公式为:
μˉ=N1i=1∑Nxi
-
期望:即一组测量数据的平均值,其并不等同于真实数据的均值,因为测量会引入误差:x~f(x)
x∼f(x)⇒E(x)=⎩⎪⎪⎪⎨⎪⎪⎪⎧N1∑i=1Nxi∑i=1∞xiPi→离散形式−∞∫+∞xf(x)dx→连续形式
(x, y)∼f(x, y)⇒{E(x)=∫−∞+∞∫−∞+∞xf(x, y)dxdyE(y)=∫−∞+∞∫−∞+∞yf(x,y)dxdy
-
常数的期望还是常数:$$E©=C$$
-
X是一个随机变量,C是常数:$$E(CX)=CE(X)$$
-
X,Y是两个随机变量,则$$E(X+Y)=E(X)+E(Y)$$
-
X,Y是两个对立变量,则$$E(XY)=E(X)E(Y)$$
-
方差:用于衡量数据与均值的偏离程度:
σ2=N1i=1∑N(xi−μ)2
-
定义:设X是一个随机变量,若$$E{[X-E(X)]^2}$$存在,则称其为X的方差,即为$$D(X)$$
-
计算公式:
D(X)=E(x2)−E(x)2
-
常数的方差是0,$$D©=0$$,$$D(C+X)=D(X-C)=D(X)$$
-
D(CX)=C2D(X)
-
D(X+Y)=D(X)+D(Y)+2COV(X,Y)
-
D(X−Y)=D(X)+D(Y)−2COV(X,Y)
-
标准差:即为方差的平方根:
σ=N1i=1∑N(xi−μ)2
-
协方差:有两个随机变量X、Y,其协方差可通过下面的公式进行计算:
COV(X,Y)=E{[X−E(X)][Y−E(Y)]}
COV(X, Y)=E(XY)−μxμy
-
如果随机变量X、Y为独立变量,那么其两者的协方差计算值为0
-
COV(X,X)=D(X)
-
COV(X,Y)=COV(Y,X)
-
COV(aX,bY)=abCOV(X,Y)
-
COV(X1+X2,bY)=COV(X1,Y)+COV(X2,Y)
-
相关系数的定义:
ρXY=D(X)D(Y)COV(X, Y)
-
高斯正态分布:
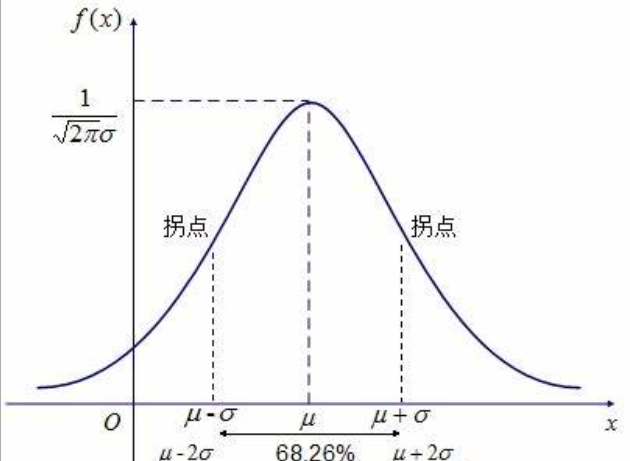
f(x, μ, σ2)=2πσ21e2σ2−(x−μ)2
第二章 基本定义
第二部分 一维卡尔曼滤波
- 引入的噪声符合高斯正态分布;
- 当前时刻状态只和上一时刻状态有关;
- 模型和系统均满足线性关系;
第一章 状态更新方程
第一节 应用场景
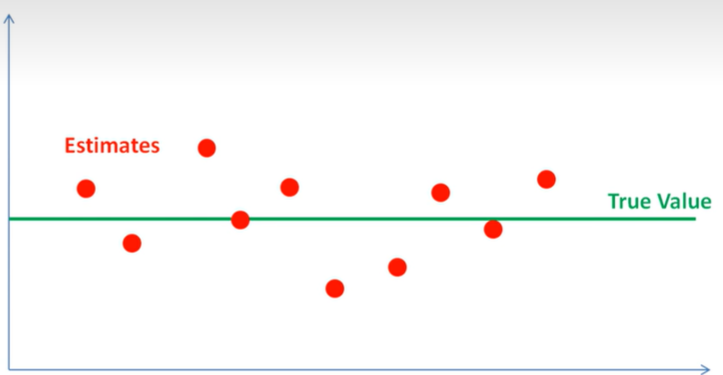
- 传感器待测参数为静态值,其不随时间的变化而变化;
- 传感器测量偏差较小,但测量引入了随机噪声;
-
均值法:一个很容易理解的方法就是根据所有的测量值求均值即可削减噪声的影响。但是在实际应用中,每次获得传感器数据后求取均值操作的运算量和所占内存都很多,因此不太实用;
μˉ=N1i=1∑Nxi
-
卡尔曼状态估计方程:为了利于编程将均值法改为递推法求取,以减少运算量和内存占用量:
第二节 公式基本推导
-
变量定义:
-
公式推导:
x^n∣n=n1i=1∑nzi
x^n∣n=n1(i=1∑n−1zi+zn)=n1i=1∑n−1zi+n1zn
x^n∣n=n1n−1n−1i=1∑n−1zi+n1zn=nn−1n−11i=1∑n−1zi+n1zn
x^n∣n=nn−1x^n∣n−1+n1zn=x^n∣n−1−n1x^n∣n−1+n1zn
x^n∣n=x^n∣n−1+n1(zn−x^n∣n−1)
-
程序流程图:
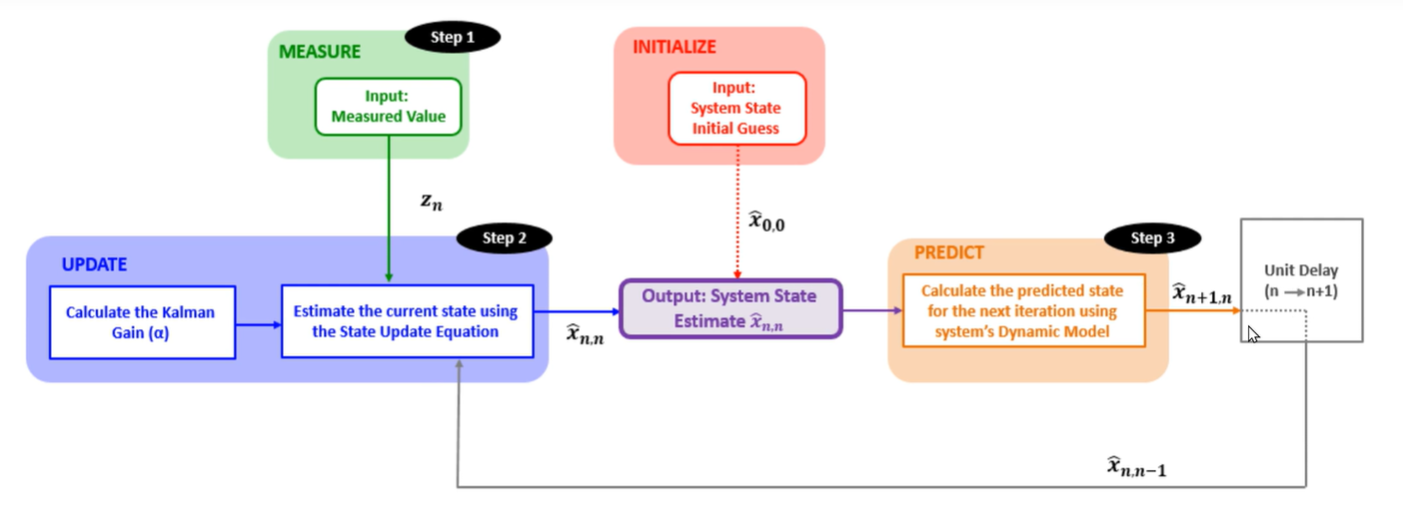
第二章 状态预测方程
前一章推导状态更新方程时,假设其为静态系统,即传感器待测参数不随时间发生变化,但是在某些情况下其待测参数是会随着时间的变化而发生改变的,因此需要引入状态外推方程,以根据当前时刻信息来预测下一时刻的信息。
第一节 应用场景
-
有一个质点沿着某一条直线做匀速直线运动,此系统中存在某一个传感器其可测量出当前时刻下质点的位置信息,周期为Δt,依据描述可建立系统的描述方程组如下所示:
{xn+1=xn+x˙nΔtx˙n+1=x˙n
第二节 公式推导
-
状态预测方程:即根据当前时刻的信息与系统的数学模型来外推下一时刻的输出。
-
状态更新方程:由于传感器测量存在噪声,因此需要在状态更新方程中引入调整因子来衡量传感器测量和模型预算的所占比例,以不断迭代计算出准确的系统状态:
x^n∣n=x^n∣n−1+Keq(zn−x^n∣n−1)
当前时刻的估计值=前一时刻对当前时刻的先验估计值+卡尔曼增益(当前时刻测量值−前一时刻对当前时刻的先验估计值)
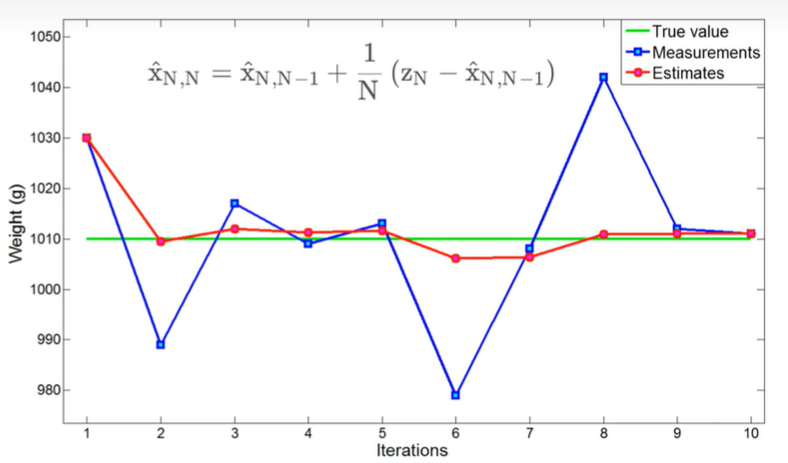
以静态系统且不考虑过程噪声为例,依据上述给出的状态更新方程,即可估计出参数值,随着测量次数的不断增加,估计值逐渐收敛于真实值;
-
测量误差:传感器测量误差可以使用反差进行描述,其值可由传感器供应商提供,其描述了测量的不确定性;
-
估计不确定性:尽管随着测量次数的增加,估计值不断收敛于测量值,但是其与真实值之间的误差无法求取,但是可以使用一个概率值P以描述估计的不确定性。
-
外推估计的不确定性:在每次估计值时需要通过系统模型外推下一时刻的系统状态值,因此估计的不确定存在传递现象。
-
引入测量误差和估计不确定性后卡尔曼滤波状态更新方程:w1为权重因子
x^n∣n=w1x^n∣n−1+(1−w1)x^n∣n−1
Pn∣n=w12rn+(1−w1)2Pn∣n−1
1
2
3
| @Pn|n:第n次估计的不确定性(方差)
@rn:传感器的测量方差
@Pn|n-1:由n-1时刻估计出的估计的当前时刻估计不确定性值(方差)
|
-
卡尔曼滤波要使其估计不确定最小,可对其求导:
dw1dPn∣n=2w1rn+2(1−w1)Pn∣n−1=0
w1=Pn∣n−1+rnPn∣n−1
第三章 卡尔曼增益方程
-
卡尔曼滤波要使其估计不确定最小,可对其求导:
dw1dPn∣n=2w1rn+2(1−w1)Pn∣n−1=0
w1=Pn∣n−1+rnPn∣n−1
-
整理卡尔曼状态更新方程为:
x^n∣n=x^n∣n−1+Kn(zn−x^n∣n−1)
-
卡尔曼增益计算方程为:
Kn=Pn∣n−1+rnPn∣n−1
Kn=估计不确定性+测量不确定性估计不确定性
第四章 协方差更新方程
第五章 协方差预测方程
-
预测方程与系统模型相关,以第二章示例进行说明,其协方差外推方程为:
{Pn+1∣nx=Pn∣nx+Δt2Pn∣nvPn+1∣nv=Pn∣nv
-
综上可得不带过程噪声的卡尔曼滤波方程流程图如下所示:
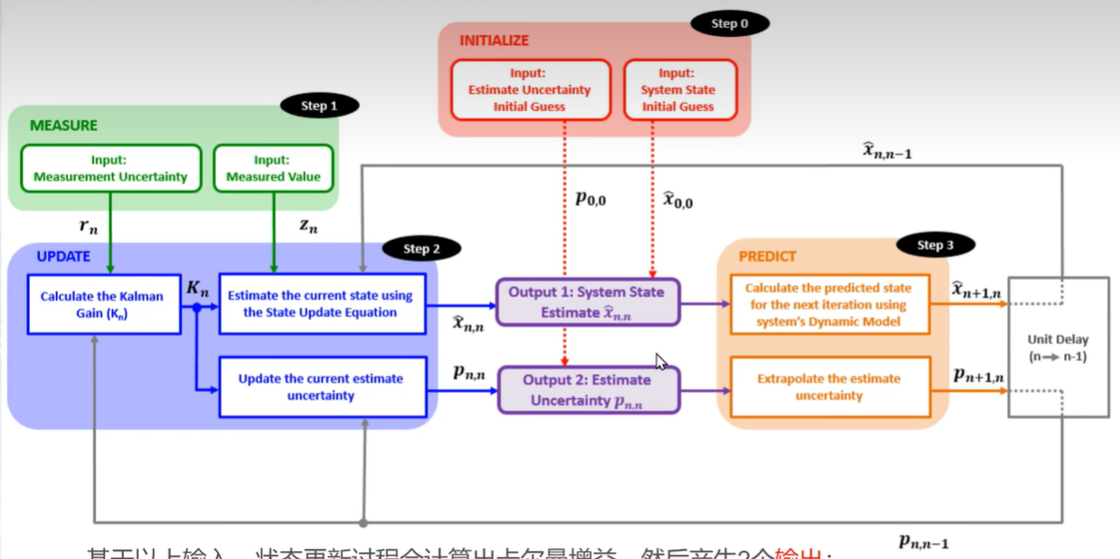
第六章 过程噪声
前面五章已经推导出来一维卡尔曼滤波的全部方程,但是其假设条件中假设整个系统不存在过程噪声,即系统的描述方程与实际应用并不是完全对应的。
-
过程噪声:以方差的形式进行标识,字母q,需要引入到协方差预测方程中,其放在系统的最高阶预测方程中。
{Pn+1∣nx=Pn∣nx+Δt2Pn∣nvPn+1∣nv=Pn∣nv+qn
第三部分 线性卡尔曼滤波
-
引入的噪声符合高斯正态分布;
-
当前时刻状态只和上一时刻状态有关;
-
模型和系统均满足线性关系;
-
控制系统的状态空间表达式为:
{x˙=Ax+Buy=Cx+Du
第一章 状态预测方程
x^n+1∣n=Fx^n∣n+Gun∣n+wn∣n
1
2
3
4
5
| @A:状态转移矩阵
@B:输入转移矩阵
@wn:过程噪声
@x:系统状态向量
@u:系统输入向量
|
-
对于无输入系统而言,其系统方程为:
x˙=Ax
-
设两次测量时间间隔为:$$ \varDelta t$$,则有:
dtdx=Ax
xdx=Adt
∫xnxn+1x1dx=∫nΔt(n+1)ΔtAdt
ln(xn+1)−ln(xn)=AΔt
xn+1=xneAΔt
F=eAΔt=I+AΔt+2!(AΔt)2+3!(AΔt)3+⋯
-
考虑有输入系统,其系统方程为:
x˙=Ax+Bu
xn+1=xneAΔt+∫nΔt(n+1)ΔteAtdtBu(t)
{F=eAΔt=I+AΔt+2!(AΔt)2+3!(AΔt)3+⋯G=B∫nΔt(n+1)ΔteAtdt=Δt(I+2!AΔt+3!(AΔt)2+⋯)
第二章 协方差预测方程
Pn+1∣n=FPn∣nFT+Q
1
2
3
| @P:协方差矩阵
@F:状态转移矩阵
@Q:过程噪声矩阵
|
-
设状态向量x有n个元素,则有状态向量x的协方差矩阵为:
COV(x)=E⎝⎜⎜⎜⎛⎣⎢⎢⎢⎡D(x1)COV(x2,x2)⋯COV(xn,x1)COV(x1,x2)D(x2)⋯COV(xn,x2)⋯⋯⋯⋯COV(x1,xn)COV(x2,xn)⋯D(xn)⎦⎥⎥⎥⎤⎠⎟⎟⎟⎞
-
不考虑过程噪声:
-
已知协方差状态转移矩阵计算公式如下:
Pn∣n=E((x^n,n−μxn,n)(x^n,n−μxn,n)T)
-
则可得:
Pn+1∣n=E((x^n+1,n−μxn+1,n)(x^n+1,n−μxn+1,n)T)
Pn+1∣n=E((Fx^n∣n+Gun∣n−Fμxn,n−Gun∣n)(Fx^n∣n+Gun−Fμxn,n−Gun∣n)T)
Pn+1∣n=E(F(x^n∣n−μxn,n)(x^n∣n−μxn,n)TFT)
Pn+1∣n=FE((x^n∣n−μxn,n)(x^n∣n−μxn,n)T)FT
Pn+1∣n=FPn∣nFT
-
考虑过程噪声:
-
一般在状态预测方程中并不考虑过程噪声的作用,而在协方差预测方程中进行考虑(直接加进去),其以噪声矩阵Q的形式来表示:
Qn=E(wnwnT)
Q=⎣⎢⎢⎢⎡q110⋯00q22⋯0⋯⋯⋯⋯00⋯qnn⎦⎥⎥⎥⎤
1
| @每个状态变量的过程噪声可以是独立的,其取决于状态变量之间是否存在一定的作用关系。若状态变量之间互相独立则其仅有主对角线上有元素。
|
第三章 状态测量方程
zn=Hxn+vn
1
2
3
4
| @Zn:观测向量
@H:观测矩阵
@xn:真实系统状态
@vn:随机噪声向量
|
-
有的时候状态向量可能并不能直接用传感器设备测量出来,其一般通过传感器测量其他物理量并通过观察矩阵以实现物理量之间的耦合表示。
-
随机噪声向量是不可知的,因此一般不在这考虑噪声而在协方差矩阵方程中考虑噪声的不确定性。
-
测量不确定性:
Rn=E(vnvnT)
第四章 状态更新方程
x^n∣n=x^n∣n−1+Kn(zn−Hx^n∣n−1)
1
2
3
4
5
| @xnn:当前时刻状态值的估计值
@xnn-1:前一时刻对当前时刻状态值的预测
@Kn:卡尔曼增益
@zn:测量值
@H:观测矩阵
|
第五章 协方差更新方程
Pn∣n=(I−KnH)Pn∣n−1(I−KnH)T+KnRnKnT
1
2
3
4
| @Pnn:协方差矩阵
@Kn:卡尔曼增益
@H:观察矩阵
@Rn:测量不确定性
|
-
公式推导:
en=xn−x^n∣n−1−Kn(zn−Hx^n∣n−1)
en=xn−x^n∣n−1−Kn(Hxn+vn−Hx^n∣n−1)
en=xn−x^n∣n−1−KnHxn−Knvn+KnHx^n∣n−1
en=xn−x^n∣n−1−KnH(xn−x^n∣n−1)−Knvn
en=(I−KnH)(xn−x^n∣n−1)−Knvn
Pn∣n=E(enenT)=E((xn−x^n∣n)(xn−x^n∣n)T)
Pn∣n=E(((I−KnH)(xn−x^n∣n−1)−Knvn)((I−KnH)(xn−x^n∣n−1)−Knvn)T)
Pn∣n=E((I−KnH)(xn−x^n∣n−1)(xn−x^n∣n−1)T(I−KnH)T)−E((I−KnH)(xn−x^n∣n−1)(Knvn)T)−E(Knvn(xn−x^n∣n−1)T(I−KnH)T)+E(Knvn(Knvn)T)
Pn∣n=E((I−KnH)(xn−x^n∣n−1)(xn−x^n∣n−1)T(I−KnH)T)+E(KnvnvnTKnT)
Pn∣n=(I−KnH)E((xn−x^n∣n−1)(xn−x^n∣n−1)T)(I−KnH)T+KnE(vnvnT)KnT
Pn∣n=(I−KnH)Pn∣n−1(I−KnH)T+KnRnKnT
第六章 卡尔曼增益方程
Kn=Pn∣n−1HT(HPn∣n−1HT+Rn)−1
1
2
3
4
| @Kn:卡尔曼滤波增益
@H:观察矩阵
@Pnn-1:状态的协方差矩阵
@Rn:测量噪声的协方差矩阵
|
-
为了最小化当前状态的协方差矩阵最小,那么需要最小化协方差矩阵的主对角线元素最小,由于主对角线元素的和成为方阵的迹,因此需要对迹Pnn求关于Kn的微分:
Pn∣n=(I−KnH)Pn∣n−1(I−KnH)T+KnRnKnT
Pn∣n=(I−KnH)Pn∣n−1(I−HTKNT)+KnRnKnT
Pn∣n=(Pn∣n−1−KnHPn∣n−1)(I−HTKNT)+KnRnKnT
Pn∣n=Pn∣n−1−Pn∣n−1HTKNT−KnHPn∣n−1+KnHPn∣n−1HTKNT+KnRnKnT
Pn∣n=Pn∣n−1−Pn∣n−1HTKNT−KnHPn∣n−1+Kn(HPn∣n−1HT+Rn)KNT
-
协方差矩阵是对阵矩阵,所以其转置等于他本身;
-
转置矩阵的迹和其矩阵的迹相等;
-
对上式求迹可得:
tr(Pn∣n)=tr(Pn∣n−1)−tr(Pn∣n−1HTKNT)−tr(KnHPn∣n−1)+tr(Kn(HPn∣n−1HT+Rn)KNT)
tr(Pn∣n)=tr(Pn∣n−1)−tr(KnHPn∣n−1)−tr(KnHPn∣n−1)+tr(Kn(HPn∣n−1HT+Rn)KNT)
tr(Pn∣n)=tr(Pn∣n−1)−2tr(KnHPn∣n−1)+tr(Kn(HPn∣n−1HT+Rn)KNT)
-
对上式求微分可得:
tr(Pn∣n)=tr(Pn∣n−1)−2tr(KnHPn∣n−1)+tr(Kn(HPn∣n−1HT+Rn)KNT)
dKndtr(Pn∣n)=dKndtr(Pn∣n−1)−dKnd2tr(KnHPn∣n−1)+dKndtr(Kn(HPn∣n−1HT+Rn)KNT)=0
dKndtr(Pn∣n)=0−dKnd2tr(KnHPn∣n−1)+dKndtr(Kn(HPn∣n−1HT+Rn)KNT)=0
-
引入迹微分性质:
dAd(tr(AB))=BT
dAd(tr(ABAT))=2AB
-
化简可得:
dKndtr(Pn∣n)=−2(HPn∣n−1)T+2Kn(HPn∣n−1HT+Rn)=0
(HPn∣n−1)T=Kn(HPn∣n−1HT+Rn)
Kn=(H)T(HPn∣n−1HT+Rn)−1
Kn=Pn∣n−1THT(HPn∣n−1HT+Rn)−1
Kn=Pn∣n−1HT(HPn∣n−1HT+Rn)−1
第七章 协方差更新方程的简化版本
未简化:Pn∣n=(I−KnH)Pn∣n−1(I−KnH)T+KnRnKnT
简化后:Pn∣n=(I−KnH)Pn∣n−1
-
可以将卡尔曼增益方程代入到协方差更新方程中以简化卡尔曼增益方程:
Pn∣n=(I−KnH)Pn∣n−1(I−KnH)T+KnRnKnT
Pn∣n=(I−KnH)Pn∣n−1(I−HTKNT)+KnRnKnT
Pn∣n=(Pn∣n−1−KnHPn∣n−1)(I−HTKNT)+KnRnKnT
Pn∣n=Pn∣n−1−Pn∣n−1HTKNT−KnHPn∣n−1+KnHPn∣n−1HTKNT+KnRnKnT
Pn∣n=Pn∣n−1−Pn∣n−1HTKNT−KnHPn∣n−1+Kn(HPn∣n−1HT+Rn)KNT
-
将卡尔曼增益方程代入可得:
Pn∣n=Pn∣n−1−Pn∣n−1HTKNT−KnHPn∣n−1+Pn∣n−1HT(HPn∣n−1HT+Rn)−1(HPn∣n−1HT+Rn)KNT
Pn∣n=Pn∣n−1−Pn∣n−1HTKNT−KnHPn∣n−1+Pn∣n−1HTKNT
Pn∣n=Pn∣n−1−KnHPn∣n−1
Pn∣n=(I−KnH)Pn∣n−1
第八章 卡尔曼滤波整理
-
六个方程组:
-
状态预测方程:
x^n+1∣n=Fx^n∣n+Gun∣n+wn∣n
-
协方差预测方程:
Pn+1∣n=FPn∣nFT+Q
-
状态测量方程:
zn=Hxn+vn
-
状态更新方程:
x^n∣n=x^n∣n−1+Kn(zn−Hx^n∣n−1)
-
协方差更新方程:
Pn∣n=(I−KnH)Pn∣n−1(I−KnH)T+KnRnKnT
Pn∣n=(I−KnH)Pn∣n−1
-
卡尔曼增益方程:
Kn=Pn∣n−1HT(HPn∣n−1HT+Rn)−1




