Foc电机驱动

相关仿真模型地址：ChenZR0509/FOC-: 存放FOC驱动学习过程中用到的资料以及笔记

第一部分 PMSM三相电机模型[1]

第一章 假设

  • 电机类型：永磁同步电机

  • 假设：

    1. 定子绕组为Y型联接，三相绕组对称分布，轴线互差120°;
    2. 忽略铁心饱和效应
    3. 气隙磁场成正弦分布
    4. 不考虑涡流和磁滞损耗
    5. 转子不考虑阻尼绕组，永磁体无阻尼作用
    6. 稳态运行时，相绕组中感应电动势波形为正弦波
    7. 电机长时间工作受到温度和频率影响不计
    8. 忽略电机具有的高次谐波
    9. 忽略换相过程中的电枢反应
    10. 电机类型为表贴式转子，气息磁阻分布均匀，各相电阻电感值相等
    11. 忽略电机中的铁损和漏磁

第二章 坐标系的建立

  • d-q轴坐标系：

    d-q轴坐标系

    1
    2
    3
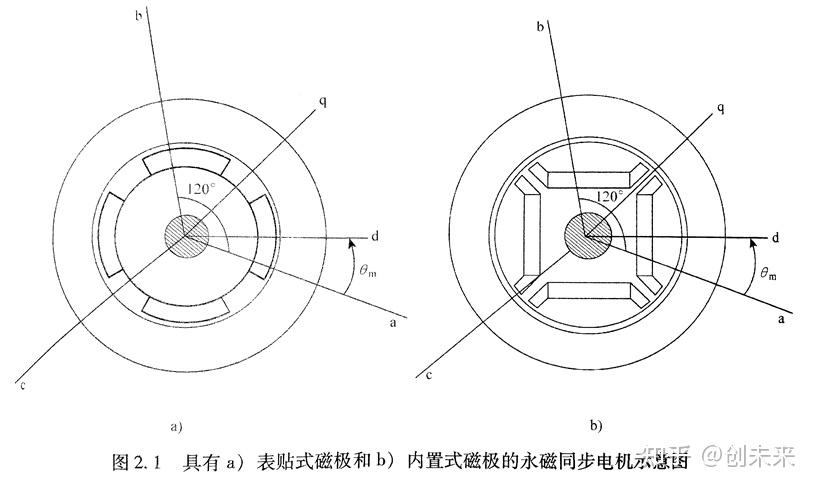
    PMSM电机其转子为永磁体，d-q轴坐标系即为磁链旋转参考坐标系(转子坐标系)，其d轴与q轴相差90°，且坐标系圆点位于转子中心，d轴位于磁极整个长度的最大磁通密度点上，这是在磁极的中心，d轴即为转子s极指向n极的方向。d-q轴固定在转子上并跟随转子旋转。
    @d轴：直轴，此方向上的电流分量主要是产生励磁的作用。
    @q轴：交轴，此方向上的电流分量主要产生转矩的作用。

  • 静止坐标系a-b-c：

    1
    静止坐标系固定，且原点与转子的旋转坐标系重合。

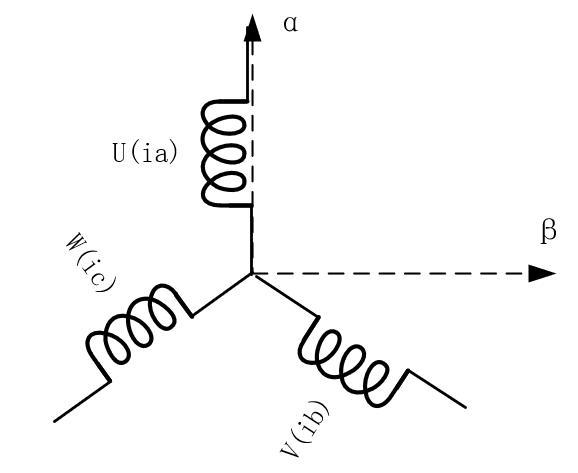
  • 静止坐标系α-β：

    1
    静止坐标系固定，且原点与转子的旋转坐标系重合。α轴与a轴重合，β与α轴相差90°

第三章 静止坐标系a-b-c下的模型

  • 旋转的矢量：

    {us→=us‾ejwetis→=is‾ejwetψs→=ψs‾ejwet\left\{ \begin{array}{l} \overrightarrow{u_s}=\overline{u_s}e^{jw_et}\\ \overrightarrow{i_s}=\overline{i_s}e^{jw_et}\\ \overrightarrow{\psi _s}=\overline{\psi _s}e^{jw_et}\\ \end{array} \right. 

    1
    2
    3
    4
    5
    6
    7
    @电机旋转过程中，矢量也在进行旋转为了以数学的形式表达旋转的矢量，做以下定义：
    	1、箭头表示旋转的矢量
    	2、横线表示矢量
    @we：表示旋转时电角速度
    @us：定子电压，这里us代表的是ua、ub、uc
    @is：定子电流，这里is代表的是ia、ib、ic
    @ψs：定子绕组磁链，这里ψs代表的是ψa、ψb、ψc

  • 磁路分析：

    • 定子绕组磁链：

      ψc→=Lsis→=Lsis‾ejwet\overrightarrow{\psi _c}=L_s\overrightarrow{i_s}=L_s\overline{i_s}e^{jw_et} 

      1
      2
      3
      @Ls：定子的电感，这里Ls代表的是La、Lb、Lc
      @is：流经定子的电流，这里is代表的是ia、ib、ic
      @we：电角速度

    • 转子绕组磁链：

      ψf→=ψf‾ejwet\overrightarrow{\psi _f}=\overline{\psi _f}e^{jw_et} 

      1
      2
      @ψf：转子磁链
      @we：电角速度

    • 电机总磁链：

      ψs→=ψc→+ψf→\overrightarrow{\psi _s}=\overrightarrow{\psi _c}+\overrightarrow{\psi _f} 

      1
      2
      3
      @ψs：电机磁链
      @ψc：定子磁链
      @ψf：转子磁链

  • 电路分析：

    us→=Rsis→+dψs→dt\overrightarrow{u_s}=R_s\overrightarrow{i_s}+\frac{d\overrightarrow{\psi _s}}{dt} 

    1
    @定子电压=定子等效电阻压降+磁链变化产生的压降

    us→=Rsis→+Lsdis→dt+jweψf→\overrightarrow{u_s}=R_s\overrightarrow{i_s}+L_s\frac{d\overrightarrow{i_s}}{dt}+jw_e\overrightarrow{\psi _f} 

    1
    @定子电压=定子等效电阻压降+定子等效电感压降+转子磁场变换作用在定子上产生的压降

  • 转矩分析：

    P→=<us→ , is→>=us→⋅is∗→\overrightarrow{P}=\left< \overrightarrow{u_s}\ ,\ \right. \left. \overrightarrow{i_s} \right> =\overrightarrow{u_s}\cdot \overrightarrow{i_s^*} 

    1
    @电机功率计算，将式6带入可得

    第一项：Rsis→⋅is∗→=Rsis‾ejwet⋅is∗‾e−jwet=Rs∣is∣2第一项：R_s\overrightarrow{i_s}\cdot \overrightarrow{i_{s}^{*}}=R_s\overline{i_s}e^{jw_et}\cdot \overline{i_s^*}e^{-jw_et}=R_s\left| i_s \right|^2 

    1
    @定子绕组在电流的作用下产生的热功率

    第二项：dψs→dt⋅is∗→=jweψs‾ejwet⋅is∗‾e−jwet=jweψs‾is∗‾=⌊ψs‾⌋∣is∗‾∣(∠ψs‾−∠is‾)第二项：\frac{d\overrightarrow{\psi _s}}{dt}\cdot \overrightarrow{i_{s}^{*}}=jw_e\overline{\psi _s}e^{jw_et}\cdot \overline{i_{s}^{*}}e^{-jw_et}=jw_e\overline{\psi _s}\overline{i_{s}^{*}}=\lfloor \overline{\psi _s} \rfloor \left| \overline{i_{s}^{*}} \right|\left( \angle \overline{\psi _s}-\angle \overline{i_s} \right) 

    1
    2
    3
    @上面的式子是一个复功率
    @实部是有功功率：取实部就是模长×sin
    @虚部是无功功率：取实部就是模长×cos

    Pe=weψs→×is→P_e=w_e\overrightarrow{\psi _s}\times \overrightarrow{i_s}

    T→=Pewr=wewrψs→×is→=Pnψs→×is→\overrightarrow{T}=\frac{P_e}{w_r}=\frac{w_e}{w_r}\overrightarrow{\psi _s}\times \overrightarrow{i_s}=P_n\overrightarrow{\psi _s}\times \overrightarrow{i_s} 

    1
    2
    3
    4
    5
    @上面就是推导出来的电机转矩公式
    @Pe：电机有效电功率
    @we：电机的电角速率
    @wr：电机的机械角速率
    @Pn：极对数

  • 电角度和机械角度：

    • 当极对数为1的时候，电机转动一圈，电信号变换一个周期
    • 当极对数大于1的时候，电机转动一圈，电信号变换Pn个周期

    电角度与机械角度转换：θe=θmPn电角度与机械角度转换：\theta _e=\theta _mP_n

  • 电压平衡方程：

    [ua→ub→uc→]=[R000R000R][ia→ib→ic→]+ddt[ψa→ψb→ψc→]\left[ \begin{array}{c} \overrightarrow{u_a}\\ \overrightarrow{u_b}\\ \overrightarrow{u_c}\\ \end{array} \right] =\left[ \begin{matrix} R& 0& 0\\ 0& R& 0\\ 0& 0& R\\ \end{matrix} \right] \left[ \begin{array}{c} \begin{array}{c} \overrightarrow{i_a}\\ \overrightarrow{i_b}\\ \overrightarrow{i_c}\\ \end{array}\\ \end{array} \right] +\frac{d}{dt}\left[ \begin{array}{c} \begin{array}{c} \overrightarrow{\psi _a}\\ \overrightarrow{\psi _b}\\ \overrightarrow{\psi _c}\\ \end{array}\\ \end{array} \right] 

    1
    2
    3
    4
    @u：表示三相定子相电压
    @i：表示三相定子相电流
    @R：表示三相定子的电阻
    @ψ：表示三相定子的磁链

  • 磁链方程：

    [ψa→ψb→ψc→]=[LaaLbaLcaLabLbbLcbLacLbcLcc][ia→ib→ic→]+ψf→[cos⁡θecos⁡(θe−23π)cos⁡(θe+23π)]\left[ \begin{array}{c} \begin{array}{c} \overrightarrow{\psi _a}\\ \overrightarrow{\psi _b}\\ \overrightarrow{\psi _c}\\ \end{array}\\ \end{array} \right] =\left[ \begin{matrix} L_{aa}& L_{ba}& L_{ca}\\ L_{ab}& L_{bb}& L_{cb}\\ L_{ac}& L_{bc}& L_{cc}\\ \end{matrix} \right] \left[ \begin{array}{c} \begin{array}{c} \overrightarrow{i_a}\\ \overrightarrow{i_b}\\ \overrightarrow{i_c}\\ \end{array}\\ \end{array} \right] +\overrightarrow{\psi _f}\left[ \begin{array}{c} \begin{array}{c} \cos \theta _e\\ \cos \left( \theta _e-\frac{2}{3}\pi \right)\\ \cos \left( \theta _e+\frac{2}{3}\pi \right)\\ \end{array}\\ \end{array} \right] 

    1
    2
    3
    4
    5
    6
    @Laa、Lbb、Lcc：表示三相绕组自感
    @Lxy：表示三相绕组任意两个绕组的互感
    @ψf：表示永磁体磁链
    @θe：表示电角度，即d轴与a轴的空间电角度也可以说是转子N极和A相轴线之间的夹角
    @ia、ib、ic：三相定子电流
    @ψa、ψb、ψc：表示三相绕组的磁链

    定子电感计算公式:[LaaLbaLcaLabLbbLcbLacLbcLcc]=[Laa111Lbb111Lcc][1cos⁡23πcos⁡43πcos⁡23π1cos⁡23πcos⁡43πcos⁡23π1]+[LIaLIbLIc]定子电感计算公式:\left[ \begin{matrix} L_{aa}& L_{ba}& L_{ca}\\ L_{ab}& L_{bb}& L_{cb}\\ L_{ac}& L_{bc}& L_{cc}\\ \end{matrix} \right] =\left[ \begin{matrix} L_{aa}& 1& 1\\ 1& L_{bb}& 1\\ 1& 1& L_{cc}\\ \end{matrix} \right] \left[ \begin{matrix} 1& \cos \frac{2}{3}\pi& \cos \frac{4}{3}\pi\\ \cos \frac{2}{3}\pi& 1& \cos \frac{2}{3}\pi\\ \cos \frac{4}{3}\pi& \cos \frac{2}{3}\pi& 1\\ \end{matrix} \right] +\left[ \begin{array}{c} L_{Ia}\\ L_{Ib}\\ L_{Ic}\\ \end{array} \right] 

    1
    2
    3
    @Laa、Lbb、Lcc：表示三相绕组自感
    @Lxy：表示三相绕组任意两个绕组的互感
    @Lia、Lib、Lic：表示三相绕组的漏感

  • 转矩方程：

    Te=12Pnddθm([ia→ib→ic→][ψA→ψB→ψC→])T_e=\frac{1}{2}P_n\frac{d}{d\theta _m}\left( \left[ \begin{matrix} \overrightarrow{i_a}& \overrightarrow{i_b}& \overrightarrow{i_c}\\ \end{matrix} \right] \left[ \begin{array}{c} \overrightarrow{\psi _A}\\ \overrightarrow{\psi _B}\\ \overrightarrow{\psi _C}\\ \end{array} \right] \right) 

    1
    2
    3
    4
    @极对数Pn：极数的一半
    @机械角度θm：转子相对于定子旋转的度数其体现在实际电机工作现象中。
    @ia、ib、ic：三相定子电流
    @ψa、ψb、ψc：表示三相绕组的磁链

  • 机械运动方程：

    Jdwmdt=Te−TL−BwmJ\frac{dw_m}{dt}=T_e-T_L-Bw_m 

    1
    2
    3
    4
    5
    @J：转动惯量
    @wm：机械角速度
    @B：阻尼系数
    @Te：电机转矩
    @Tl：负载转矩

第四章 静止坐标系α-β下的模型

  • Clarke变换【基于等幅值变换，所以需要添加一个2/3的系数，后面会在svpwm中消去】：

    T3sTo2s=23[1−12−12032−32]T_{3sTo2s}=\frac{2}{3}\left[ \begin{matrix} 1& -\frac{1}{2}& -\frac{1}{2}\\ 0& \frac{\sqrt{3}}{2}& -\frac{\sqrt{3}}{2}\\ \end{matrix} \right]

  • Clarke反变换：

    T2sTo3s=32[230−1333−13−33]T_{2sTo3s}=\frac{3}{2}\left[ \begin{matrix} \frac{2}{3}& 0\\ \frac{-1}{3}& \frac{\sqrt{3}}{3}\\ \frac{-1}{3}& \frac{-\sqrt{3}}{3}\\ \end{matrix} \right]

第五章 转子坐标系d-q下的模型

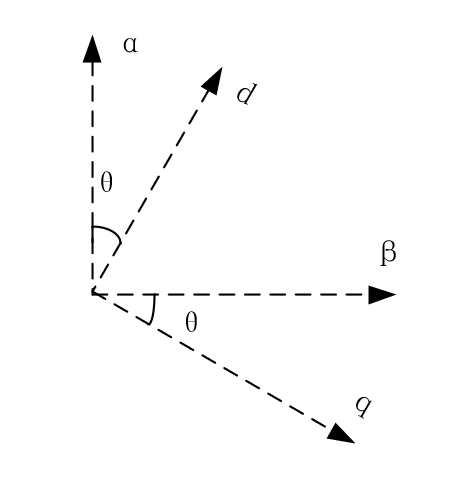
  • Park变换：

    T2sTo2d=[cos⁡θsin⁡θ−sin⁡θcos⁡θ]T_{2sTo2d}=\left[ \begin{matrix} \cos \theta& \sin \theta\\ -\sin \theta& \cos \theta\\ \end{matrix} \right]

  • 反Park变换：

    T2dTo2s=[cos⁡θ−sin⁡θsin⁡θcos⁡θ]T_{2dTo2s}=\left[ \begin{matrix} \cos \theta& -\sin \theta\\ \sin \theta& \cos \theta\\ \end{matrix} \right]

第六章 电机参数

  • 购买地址：【淘宝】限时满10减5 http://e.tb.cn/h.gwF52R6Ez6yGVWh?tk=z0uh3mNxTE8 MF6563 「微型中空无刷电机低能耗直流12V外转子空心轴旋转马达三相可调速」

  • Simulink仿真电机模型参数：

    • 电机相数：3
    • 反电动势波形：正弦波
    • 机械输入方式：负载转矩
    • 转子类型：圆柱形

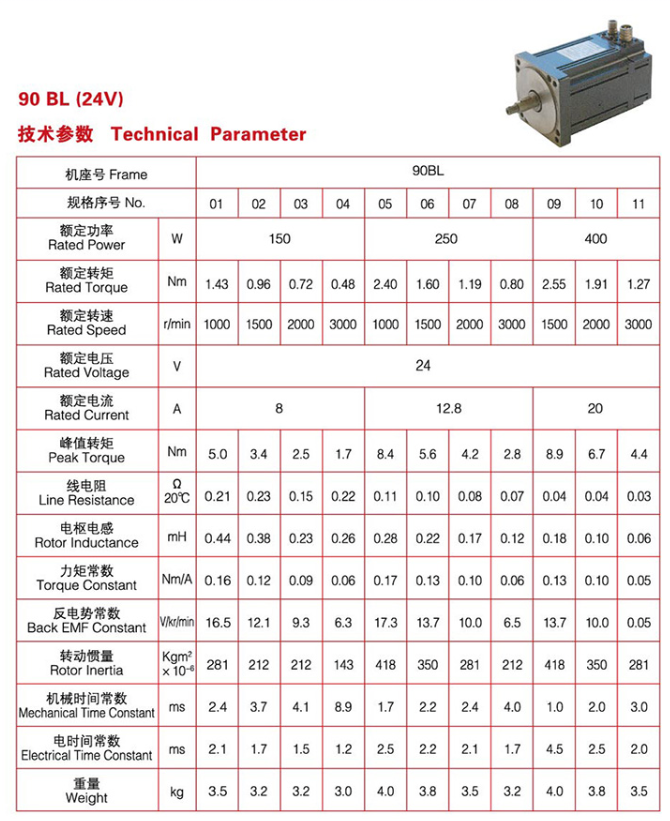
    image-20241031150145833

  • 控制要求：

    • 水平转动范围：0°~360°
    • 俯仰转动范围：-10°~50°
    • 供电电压：24V
    • 最高转速：2000转/分
    • 转速变换率：小于0.5%
    • 正反转差率：小于0.5%
    • 转速响应时间：小于40ms
    • 超调量：小于8%

第二部分 Foc的PI电流环仿真

  • 电流环作用：实现对电机电流的精确控制、加快系统的动态调节过程，使得电机定子电流可以更好地接近给定的电流矢量。

  • 电流环的组成：电机、功率放大器、电流环控制器、电流检测元件

  • 仿真搭建注意事项：

    1. 单片机的浮点运算单元只能处理单精度浮点型变量，所以在simulink仿真时进行数据转换。

第一章 数学分析

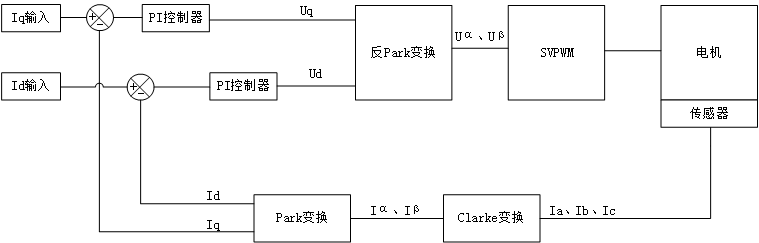
  • d-q轴电压方程：

    {Ud=RId+LddIddt−weLqIqUq=RIq+LqdIqdt+we(LdId+Ψf)\left\{ \begin{array}{l} U_d=RI_d+L_d\frac{dI_d}{dt}-w_eL_qI_q\\ U_q=RI_q+L_q\frac{dI_q}{dt}+w_e\left( L_dI_d+\varPsi _f \right)\\ \end{array} \right.

    将耦合项当作扰动项进行处理：

    {Ud0=RId+LddIddtUq0=RIq+LqdIqdt\left\{ \begin{array}{l} U_{d0}=RI_d+L_d\frac{dI_d}{dt}\\ U_{q0}=RI_q+L_q\frac{dI_q}{dt}\\ \end{array} \right.

  • d-q轴电磁转矩方程：

    Te=32PnIq[Id(Ld−Lq)+Ψf]T_e=\frac{3}{2}P_nI_q\left[ I_d\left( L_d-L_q \right) +\varPsi _f \right]

  • 由于PMSM电机为表贴式电机，有Ld=Lq=L，且d轴电流对转矩的产生不起作用，为了使得相同转矩条件下所需的电流最小，所以采用Id=0的控制策略。

{Ud0=RId+LddIddt=0Uq0=RIq+LqdIqdt=Uq−weψfTe=32PnIqΨfdwmdtJ=Te−TL−Bwm\left\{ \begin{array}{l} U_{d0}=RI_d+L_d\frac{dI_d}{dt}=0\\ U_{q0}=RI_q+L_q\frac{dI_q}{dt}=U_q-w_e\psi _f\\ T_e=\frac{3}{2}P_nI_q\varPsi _f\\ \frac{dw_m}{dt}J=T_e-T_L-Bw_m\\ \end{array} \right.

  • 对上面的式子进行拉普拉斯变换：

    {Gc(s)=Iq(s)Uq0(s)=1Ls+RGs(s)=wm(s)Te−TL=1Js+B\left\{ \begin{array}{l} G_c\left( s \right) =\frac{I_q\left( s \right)}{U_{q0}\left( s \right)}=\frac{1}{Ls+R}\\ G_s\left( s \right) =\frac{w_m\left( s \right)}{T_e-T_L}=\frac{1}{Js+B}\\ \end{array} \right.

  • 逆变器的数学模型【等效为一个一阶惯性环节】 ：

    Ginv(s)=1Tss+1G_{inv}\left( s \right) =\frac{1}{T_ss+1} 

    1
    @Ts：表示逆变器的开关周期，因为逆变器输出与输出相等，因此增益取1

    考虑开关延时、死区时间、数字控制延时的影响，将其等效为一个延迟环节：

    Ginv(s)=e−sTdTss+1G_{inv}\left( s \right) =\frac{e^{-sT_d}}{T_ss+1}

    将延迟环节按照泰勒级数展开近似为一个一阶惯性环节：

    Ginv(s)=1(Tss+1)(Tds+1)G_{inv}\left( s \right) =\frac{1}{\left( T_ss+1 \right) \left( T_ds+1 \right)}

  • PI控制器形式：

    PI=KP+KI1sPI=K_P+K_I\frac{1}{s}

  • 电流环控制结构图：

    • 规定：

      • 机械时间常数：

        Tm=2RJ3Pn2Ψf2T_m=\frac{2RJ}{3P_n^2\varPsi _f^2}

      • 电磁时间常数：

        Tn=LRT_n=\frac{L}{R}

      • 对于武器站而言，其转动惯量较大，即机械时间常数远大于电磁时间常数，因此在分析电流环控制系统时可以对扰动项$$w_e$$、$$\psi _f$$进行忽略。

    • 仿真假设：

      1. 电机空载运行，不考虑负载转矩的作用；
      2. 由于在实际工程中，常认为电机的电流环调节过程远快于转速环的调节过程，从而忽略扰动项$$w_e$$、$$\psi _f$$的作用。

    • 忽略扰动后的控制结构图：

  • 电流环传递函数：

    G(s)=1(Tss+1)(Tds+1)(Ls+R)G\left( s \right)=\frac{1}{\left( T_ss+1 \right) \left( T_ds+1 \right) \left( Ls+R \right)}

  • 加入PI控制器后的闭环传递函数为：

    G(s)=(KP+KI1s)(1(Tss+1)(Tds+1))(1Ls+R)1+(KP+KI1s)(1(Tss+1)(Tds+1))(1Ls+R)G\left( s \right) =\frac{\left( K_P+K_I\frac{1}{s} \right) \left( \frac{1}{\left( T_ss+1 \right) \left( T_ds+1 \right)} \right) \left( \frac{1}{Ls+R} \right)}{1+\left( K_P+K_I\frac{1}{s} \right) \left( \frac{1}{\left( T_ss+1 \right) \left( T_ds+1 \right)} \right) \left( \frac{1}{Ls+R} \right)}

  • PI控制器参数整定[2]：

    • 控制系统开环传递函数为：

      G(s)=(KP+KI1s)(1(Tss+1)(Tds+1))(1Ls+R)G\left( s \right) =\left( K_P+K_I\frac{1}{s} \right) \left( \frac{1}{\left( T_ss+1 \right) \left( T_ds+1 \right)} \right) \left( \frac{1}{Ls+R} \right)

    • 将中间项拆开，由于Td与Ts取值较小，故而可以将其进行简化：

      G(s)=(KP+KI1s)(11+(Td+Ts)s)(1Ls+R)G\left( s \right) =\left( K_P+K_I\frac{1}{s} \right) \left( \frac{1}{1+\left( T_d+T_s \right) s} \right) \left( \frac{1}{Ls+R} \right)

    • 整理可得：

      G(s)=(KPLs(1+(Td+Ts)s))(s+KIKPs+RL)G\left( s \right) =\left( \frac{\frac{K_P}{L}}{s\left( 1+\left( T_d+T_s \right) s \right)} \right) \left( \frac{s+\frac{K_I}{K_P}}{s+\frac{R}{L}} \right)

    • 第一项是一个Ⅰ型系统：

      K=KPLK=\frac{K_P}{L}

      T=Td+TsT=T_d+T_s

    • 第二项需要进行消除，即使用PI控制器的零点消去被控对象的极点：

      KIKP=RL\frac{K_I}{K_P}=\frac{R}{L}

    • 整定表：

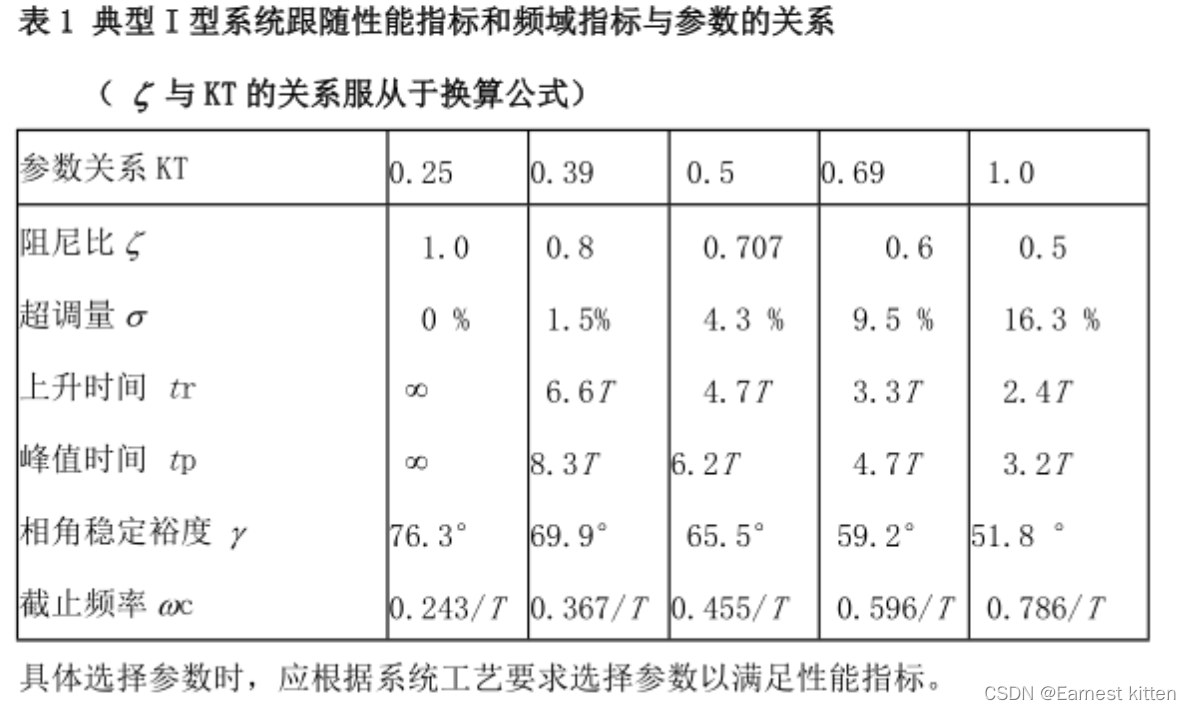
    • 当阻尼比为0.707时控制性能最好，则取KT=0.5，可得

      KP=L2(Td+Ts)K_P=\frac{L}{2\left( T_d+T_s \right)}

      KI=R2(Td+Ts)K_I=\frac{R}{2\left( T_d+T_s \right)}

第二章 Simulink仿真

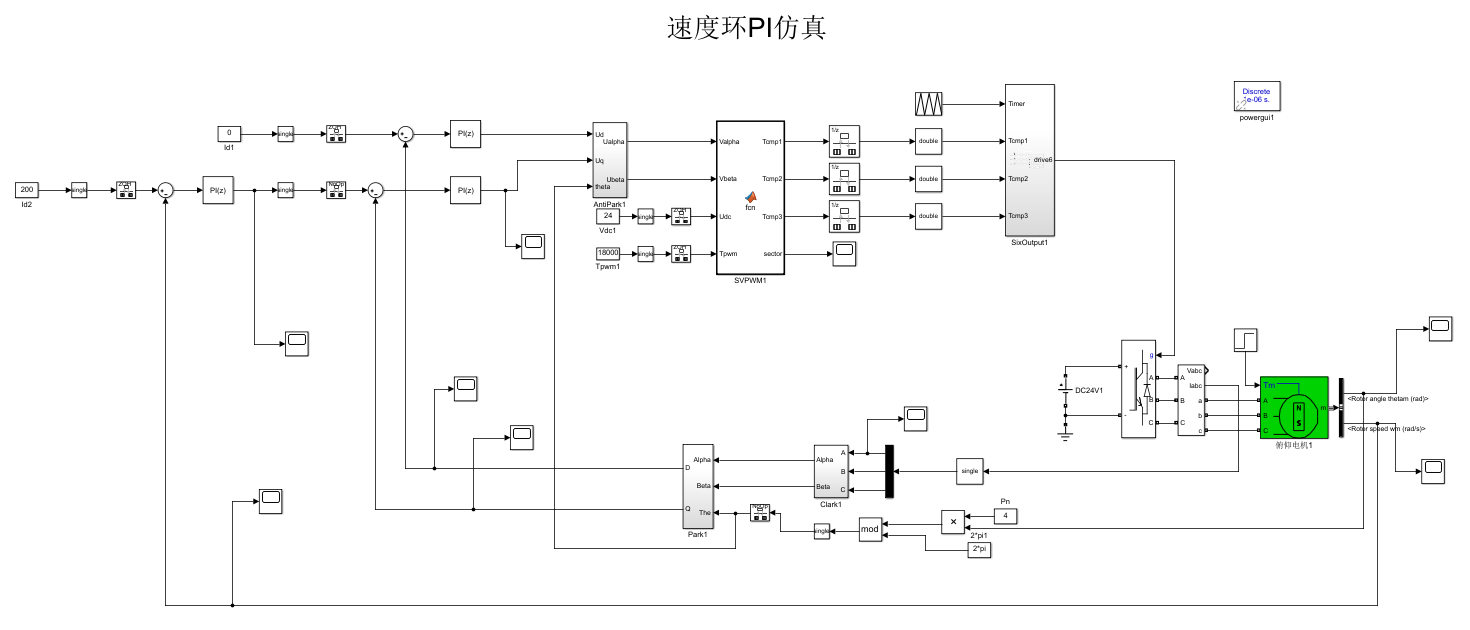
  • PI电流环仿真总览：

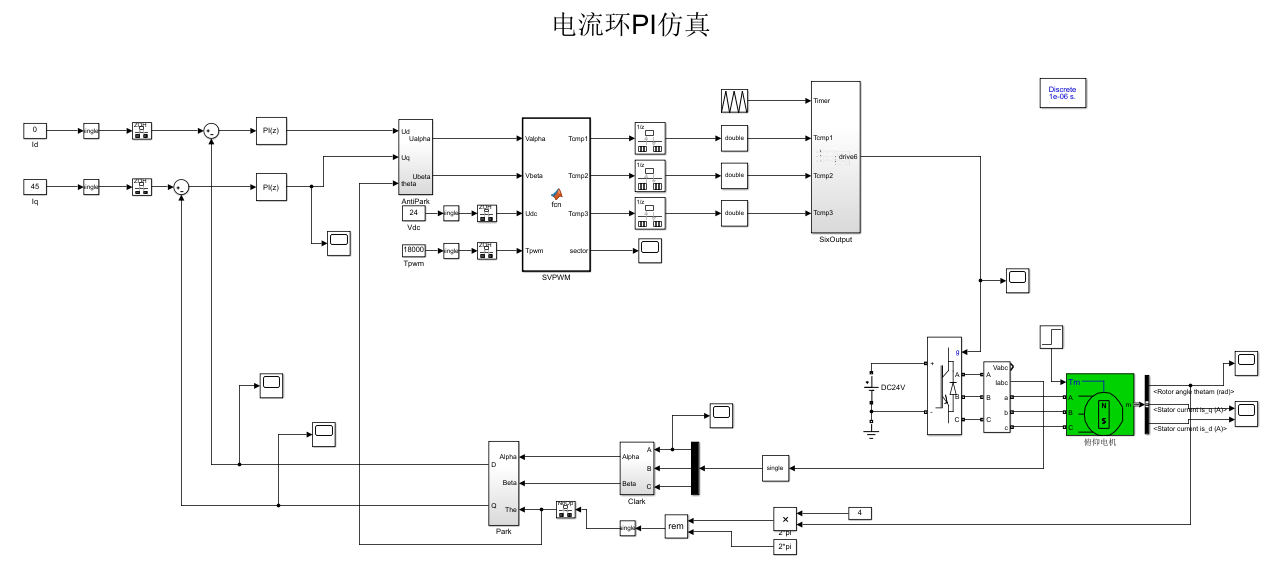
  • PMSM模块及其参数设置：

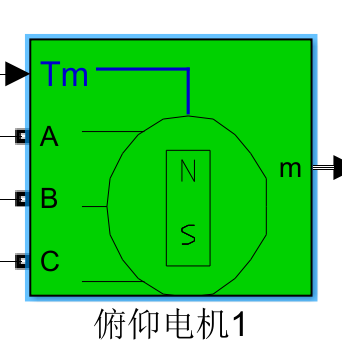
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    @配置栏：
    	@相数：3
    	@反电动势波形：正弦波
    	@转子类型：圆柱形
    	@机械输入方式：扭矩输入
    	@电机类型：No(可以自己填写参数)
    @参数栏：
    	@定子绕组阻值(Ω)：可以是一个值，也可以是一个三个元素的数组 5.8 
    	@电子绕组电感(H)：可以是一个值，也可以是一个三个元素的数组 2.55*10^-3
    	@机械常数：
    		@永磁体磁链大小(Wb)
    		@电压常数(V/krpm)	4.8
    		@扭矩常数(N·m)
    	@转动惯量(kg·m-2)、阻尼系数、极对数、静摩擦力 [0,0,7,0]
    	@电机初始状态
    @高级配置：
    	@采样时间
    	@坐标系：默认配置即可(与上面坐标系相同)

  • Clark变换仿真实现：

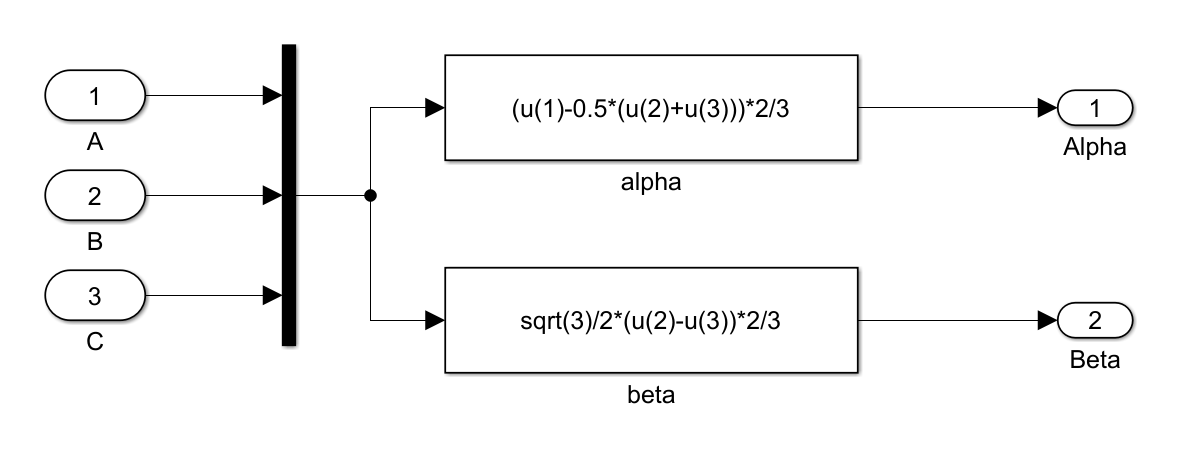
  • Park变换：

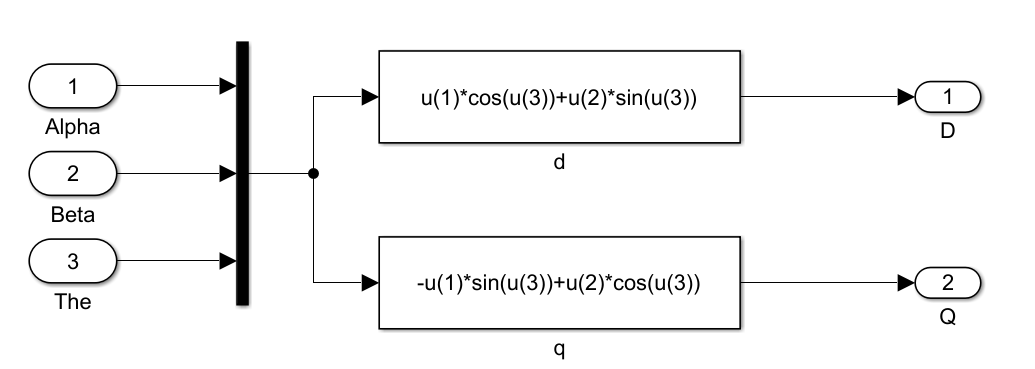
  • 反Park变换：

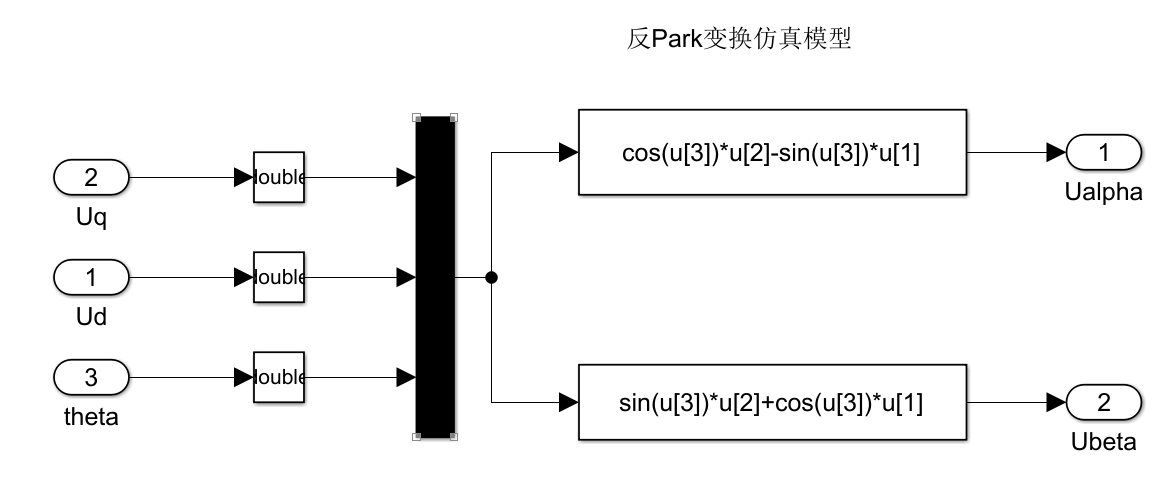
  • SVPWM：

    • 原理：根据平均值等效原理，在一个开关周期内通过对基本电压矢量加以组合，使其平均值与给定电压矢量相等。

    • 工作过程：首先，根据旋转矢量在两相静止坐标系下的分量判断其所处的扇区；然后，根据平均值等效原理计算出所在扇区主副矢量的作用时间，将其在一个开关周期内进行合理的分配并转换为对应的PWM信号，进而控制逆变器的开关。

    • 理解：

      1、想要控制转子旋转，则需要定子产生旋转的磁场，才能使得转子连续的旋转，而旋转的磁场需要正弦电流，那么如果使得直流电源产生正弦电流呢？【逆变–电力电子】

      2、六步换向每种开关状态对应一个60°的角度转动，那么如果我们缩短每次开关状态的时间，在宏观的观察上是不是就能达到小于60°的控制效果。

      3、SVPWM输入：α轴和β轴上的电压输入

      4、SVPWM输出：三相单片机计数器的数

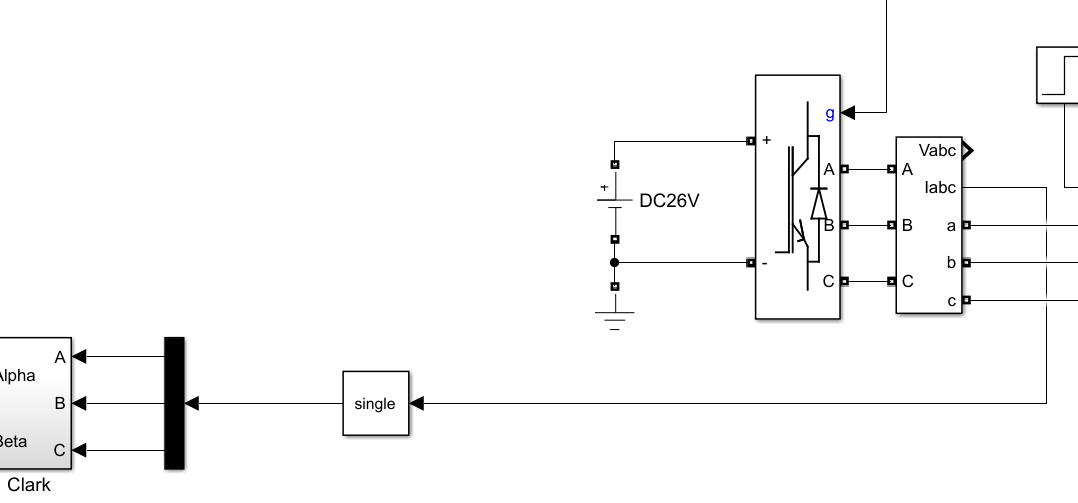
    • 六步换向原理：

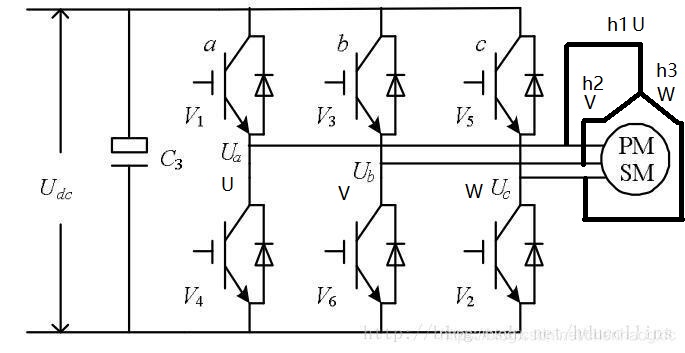
      **解释：**上半桥接直流电源正，下半桥接地。电机三个线圈采用星型接法，一端连接在一起，同时定子的三个线圈位置安装霍尔传感器以感知电机转子的转动变换。

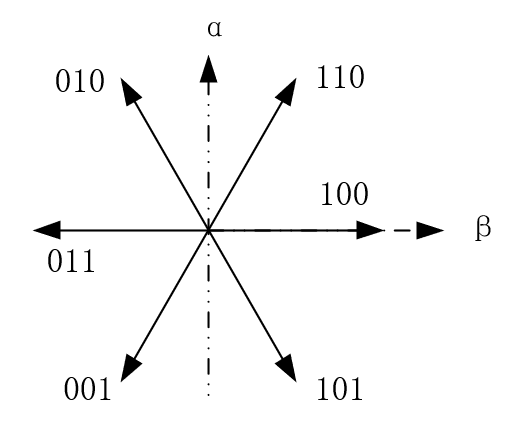
      • 六步换向驱动：其通常用来驱动直流无刷电机，直流无刷电机的定子上安装均匀安装三个霍尔编码器用以反馈转子的位置信息，当期正磁通(N---->S)流经霍尔传感器时输出为1，反之为0；

      • MOS控制：

    • SVPWM扇区判断：

      • 已知输入给三个线圈的是交流电，即正弦电压：

        {UA=Umcos⁡θUB=Umcos⁡(θ−23π)UC=Umcos⁡(θ+23π)\left\{ \begin{array}{l} U_A=U_m\cos \theta\\ U_B=U_m\cos \left( \theta -\frac{2}{3}\pi \right)\\ U_C=U_m\cos \left( \theta +\frac{2}{3}\pi \right)\\ \end{array} \right.

      • 根据Clark变换可得：

        {Uα=23Umcos⁡θUβ=23Umsin⁡θ\left\{ \begin{array}{l} U_{\alpha}=\frac{2}{3}U_m\cos \theta\\ U_{\beta}=\frac{2}{3}U_m\sin \theta\\ \end{array} \right.

      • 六步换向机制将360°分成了六个扇区，设其想要根据输入来判断所属于那个扇区那么就可以根据反三角函数来求取角度，但是反三角函数计算复杂度高不适用于单片机编程，因此需要整理一下其相关规律【将计算转换为判断与0的大小】：

        扇区 $$U_{\beta}$$ $$\frac{\sqrt{3}}{2}U_{\alpha}-\frac{1}{2}U_{\beta}$$ $$-\frac{\sqrt{3}}{2}U_{\alpha}-\frac{1}{2}U_{\beta}$$ 角度
        1 >0 >0 <0 0~60
        2 >0 <0 <0 60~120
        3 >0 <0 >0 120~180
        4 <0 <0 >0 180~240
        5 <0 >0 >0 240~300
        6 <0 >0 <0 300~360

      • 数值对应表：大于0取1，小于0取0

        {A=UβB=32Uα−12UβC=−32Uα−12Uβ\left\{ \begin{array}{l} \boldsymbol{A}=\boldsymbol{U}_{\boldsymbol{\beta }}\\ \boldsymbol{B}=\frac{\sqrt{3}}{2}U_{\alpha}-\frac{1}{2}U_{\beta}\\ \boldsymbol{C}=-\frac{\sqrt{3}}{2}U_{\alpha}-\frac{1}{2}U_{\beta}\\ \end{array} \right.

        N=4C+2B+A\boldsymbol{N}=4\boldsymbol{C}+2\boldsymbol{B}+\boldsymbol{A}

        扇区 1 2 3 4 5 6
        判据N 3 1 5 4 6 2

    • SVPWM矢量合成：

      • 六步换向产生的六个矢量大小为2/3Udc【设每个线圈阻值相同】：

        U V W Uun Uvn Uwn
        1 0 0 2/3Udc -1/3Udc -1/3Udc
        1 1 0 1/3Udc 1/3Udc -2/3Udc
        0 1 0 -1/3Udc 2/3Udc -1/3Udc
        0 1 1 -2/3Udc 1/3Udc 1/3Udc
        0 0 1 -1/3Udc -1/3Udc 2/3Udc
        1 0 1 1/3Udc -2/3Udc 1/3Udc

      • 矢量合成原理：在一段非常小的周期内，一段时间用于六步换向的一种矢量，一段时间用于六步换向的另一种相邻矢量，剩下的时间为空闲时间。这样我们就可以调节两个矢量的作用时间大小来控制矢量的大小，合成一种新的矢量。同样我们也可以固定两个矢量的时间比值，调节空闲时间的大小来调节力矩。

        1. 空矢量：000、111

        2. 矢量合成遵循平行四边形定理

        3. 周期时间表达式：

          Ts=T矢量1+T矢量2+T空闲时间T_s=T_{\text{矢量}1}+T_{\text{矢量}2}+T_{\text{空闲时间}}

        4. 两个相邻矢量作用时间推导【以扇区1为例】

          Uout=UxTxTs+UyTyTs+UnTnTsU_{out}=U_x\frac{T_x}{T_s}+U_y\frac{T_y}{T_s}+U_n\frac{T_n}{T_s}

          Uα=∣Uout∣cos⁡θ=∣Ux∣TxTs+∣Uy∣TyTscos⁡60°U_{\alpha}=\left| U_{out} \right|\cos \theta =\left| U_x \right|\frac{T_x}{T_s}+\left| U_y \right|\frac{T_y}{T_s}\cos 60^°

          Uβ=∣Uout∣sin⁡θ=∣Uy∣TyTssin⁡60°U_{\beta}=\left| U_{out} \right|\sin \theta =\left| U_y \right|\frac{T_y}{T_s}\sin 60^°

          扇区1：{Tx=3UβTsUdc(32Uα−12Uβ)Ty=3UβTsUdc扇区1： \left\{ \begin{array}{l} T_x=\sqrt{3}U_{\beta}\frac{T_s}{U_{dc}}\left( \frac{\sqrt{3}}{2}U_{\alpha}-\frac{1}{2}U_{\beta} \right)\\ T_y=\sqrt{3}U_{\beta}\frac{T_s}{U_{dc}}\\ \end{array} \right.

        5. 总结：

          扇区1：x-y

          {Tx=3UβTsUdc(32Uα−12Uβ)Ty=3UβTsUdc\left\{ \begin{array}{l} T_x=\sqrt{3}U_{\beta}\frac{T_s}{U_{dc}}\left( \frac{\sqrt{3}}{2}U_{\alpha}-\frac{1}{2}U_{\beta} \right)\\ T_y=\sqrt{3}U_{\beta}\frac{T_s}{U_{dc}}\\ \end{array} \right.

          扇区2：y-x

          {Tx=−3UβTsUdc(32Uα−12Uβ)Ty=−3UβTsUdc(−32Uα−12Uβ)\left\{ \begin{array}{l} T_x=-\sqrt{3}U_{\beta}\frac{T_s}{U_{dc}}\left( \frac{\sqrt{3}}{2}U_{\alpha}-\frac{1}{2}U_{\beta} \right)\\ T_y=-\sqrt{3}U_{\beta}\frac{T_s}{U_{dc}}\left( -\frac{\sqrt{3}}{2}U_{\alpha}-\frac{1}{2}U_{\beta} \right)\\ \end{array} \right.

          扇区3：x-y

          {Tx=3UβTsUdcTy=3UβTsUdc(−32Uα−12Uβ)\left\{ \begin{array}{l} T_x=\sqrt{3}U_{\beta}\frac{T_s}{U_{dc}}\\ T_y=\sqrt{3}U_{\beta}\frac{T_s}{U_{dc}}\left( -\frac{\sqrt{3}}{2}U_{\alpha}-\frac{1}{2}U_{\beta} \right)\\ \end{array} \right.

          扇区4：y-x

          {Tx=−3UβTsUdcTy=−3UβTsUdc(32Uα−12Uβ)\left\{ \begin{array}{l} T_x=-\sqrt{3}U_{\beta}\frac{T_s}{U_{dc}}\\ T_y=-\sqrt{3}U_{\beta}\frac{T_s}{U_{dc}}\left( \frac{\sqrt{3}}{2}U_{\alpha}-\frac{1}{2}U_{\beta} \right)\\ \end{array} \right.

          扇区5：x-y

          {Tx=3UβTsUdc(−32Uα−12Uβ)Ty=3UβTsUdc(32Uα−12Uβ)\left\{ \begin{array}{l} T_x=\sqrt{3}U_{\beta}\frac{T_s}{U_{dc}}\left( -\frac{\sqrt{3}}{2}U_{\alpha}-\frac{1}{2}U_{\beta} \right)\\ T_y=\sqrt{3}U_{\beta}\frac{T_s}{U_{dc}}\left( \frac{\sqrt{3}}{2}U_{\alpha}-\frac{1}{2}U_{\beta} \right)\\ \end{array} \right.

          扇区6：y-x

          {Tx=−3TsUdcUβTy=3UβTsUdc(32Uα+12Uβ)\left\{ \begin{array}{l} T_x=-\sqrt{3}\frac{T_s}{U_{dc}}U_{\beta}\\ T_y=\sqrt{3}U_{\beta}\frac{T_s}{U_{dc}}\left( \frac{\sqrt{3}}{2}U_{\alpha}+\frac{1}{2}U_{\beta} \right)\\ \end{array} \right.

        6. 化简：

          {X=3UβTsUdcY=3TsUdc(32Uα+12Uβ)Z=3TsUdc(32Uα−12Uβ)\left\{ \begin{array}{l} X=\sqrt{3}U_{\beta}\frac{T_s}{U_{dc}}\\ Y=\sqrt{3}\frac{T_s}{U_{dc}}\left( \frac{\sqrt{3}}{2}U_{\alpha}+\frac{1}{2}U_{\beta} \right)\\ Z=\sqrt{3}\frac{T_s}{U_{dc}}\left( \frac{\sqrt{3}}{2}U_{\alpha}-\frac{1}{2}U_{\beta} \right)\\ \end{array} \right.

          扇区 公式Tx 公式Ty
          1 -Z X
          2 Z Y
          3 X -Y
          4 -X Z
          5 -Y -Z
          6 Y -X

    • Simulink Matlab Function代码：

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      20
      21
      22
      23
      24
      25
      26
      27
      28
      29
      30
      31
      32
      33
      34
      35
      36
      37
      38
      39
      40
      41
      42
      43
      44
      45
      46
      47
      48
      49
      50
      51
      52
      53
      54
      55
      56
      57
      58
      59
      60
      61
      62
      63
      64
      65
      66
      67
      68
      69
      70
      71
      72
      73
      74
      75
      76
      77
      78
      79
      80
      81
      82
      83
      84
      85
      86
      87
      88
      89
      90
      91
      92
      %输入变量：电压Ualpha、电压Ubeta、驱动器直流供电电压Udc、输出PWM波形的周期计数值
      %输出变量：扇区、输出波形1、输出波形2、输出波形3
      function [Tcmp1,Tcmp2,Tcmp3,sector] = fcn(Valpha,Vbeta,Udc,Tpwm)

      %初始化输出变量：扇区、输出波形1、输出波形2、输出波形3
      sector = single(0);
      sectorTemp = single(0);
      Tcmp1 = single(0);
      Tcmp2 = single(0);
      Tcmp3 = single(0);

      %定义扇区三个判据表达式
      Vref1 = Vbeta;							                   
      Vref2 = (sqrt(3)*Valpha - Vbeta)/2; 				    
      Vref3 = (-sqrt(3)*Valpha - Vbeta)/2;					
      %计算扇区判据
      %sector：1   2   3   4   5   6
      %判据：  3   1   5   4   6   2
      if (Vref1>0)
          sectorTemp = single(1);
      end
      if (Vref2>0)
          sectorTemp = sectorTemp+single(2);
      end
      if (Vref3>0)
      	sectorTemp = sectorTemp+single(4);
      end

      %定义矢量合成作用时间的三个表达式判据
      X = sqrt(3)*Vbeta*Tpwm/Udc;
      Y = Tpwm/Udc*(3/2*Valpha+sqrt(3)/2*Vbeta);
      Z = Tpwm/Udc*(-3/2*Valpha+sqrt(3)/2*Vbeta);	         
      %计算占空比
      switch (sectorTemp)   
          case 1
              T1 = Z; T2 = Y; 
      	case 2
              T1 = Y; T2 = -X; 
      	case 3
              T1 = -Z; T2 = X; 
      	case 4
              T1 = -X; T2 = Z;
      	case 5
              T1 = X; T2 = -Y;
          otherwise
              T1 = -Y; T2 = -Z;
      end
      if T1+T2 > Tpwm
          T1 = T1/(T1+T2);
          T2 = T2/(T1+T2);
      else
          T1 = T1;
          T2 = T2;
      end

      %计算输出定时器计数值
      ta = (Tpwm-(T1+T2))/4.0;
      tb = ta+T1/2;
      tc = tb+T2/2;
      switch (sectorTemp)
          case 1 
              Tcmp1=tb;
              Tcmp2=ta;
              Tcmp3=tc; 
              sector = single(2);
          case 2 
              Tcmp1=ta;
              Tcmp2=tc;
              Tcmp3=tb;   
              sector = single(6);
          case 3 
              Tcmp1=ta;
              Tcmp2=tb;
              Tcmp3=tc;
              sector = single(1);
          case 4 
              Tcmp1=tc;
              Tcmp2=tb;
              Tcmp3=ta;   
              sector = single(4);
          case 5 
              Tcmp1=tc;
              Tcmp2=ta;
              Tcmp3=tb;
              sector = single(3);
         case 6
             Tcmp1=tb;
             Tcmp2=tc;
             Tcmp3=ta;
             sector = single(5);
      end
      end

    • 单片机定时器的仿真：

      • STM32F4高级定时器tim1的计数频率为：180MHz(记一个数需要1/180us)

      • PWM周期：100us（一共需要记18000个数）

      • 将单片机设置为自动递增/递减模式，那么定时器记一个周期就只需要9000个计数值。

      • 定时器时基：

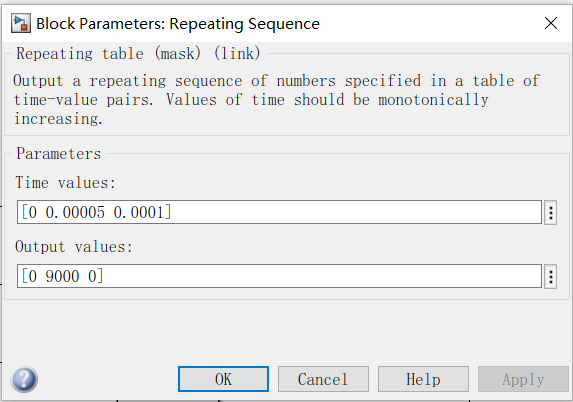
      • 定时器仿真：

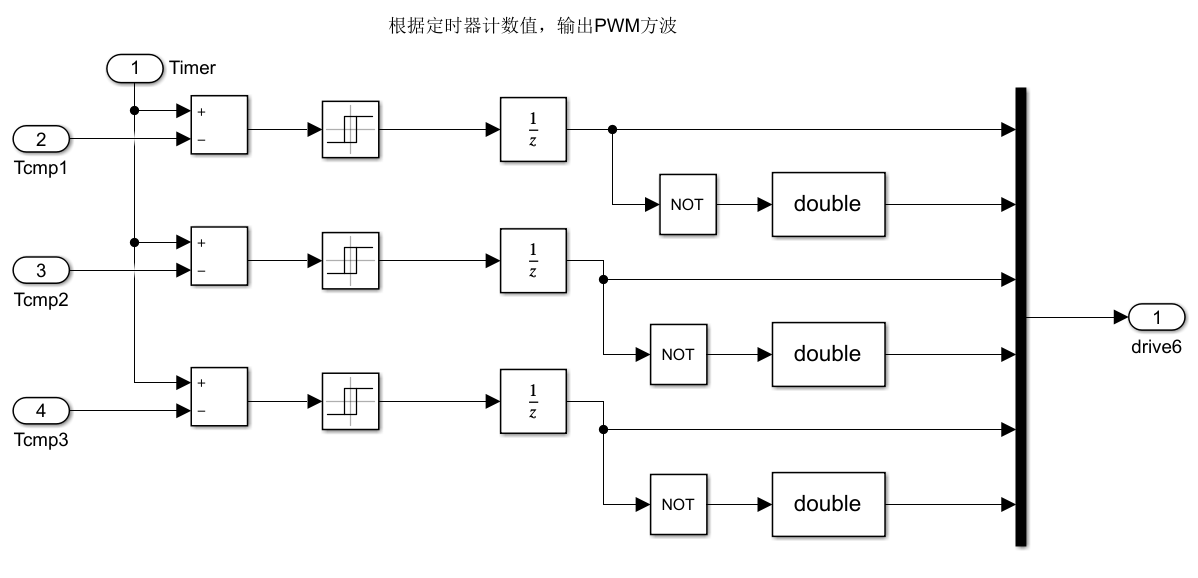
        1
        @原理：SVPWM会输出三路高低电平变换时的计数值，其与时基信号进行比较，以实现高低电平的转换，进而输出三路互补的PWM脉冲信号。

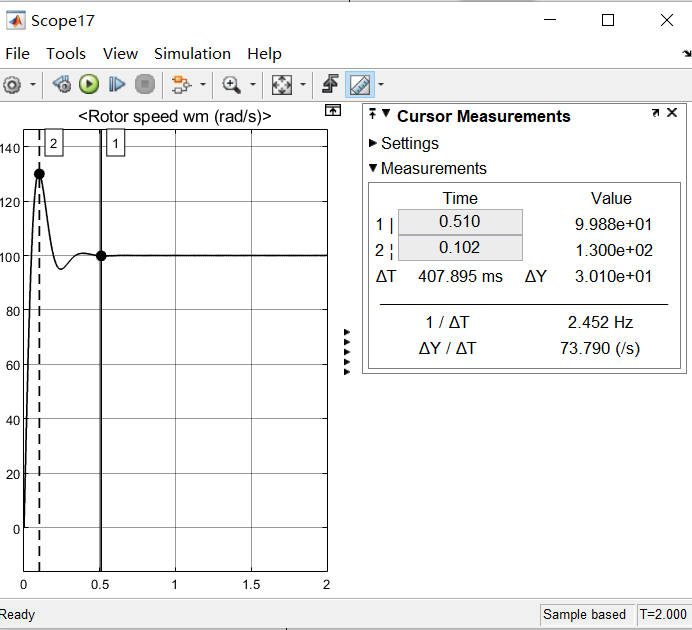
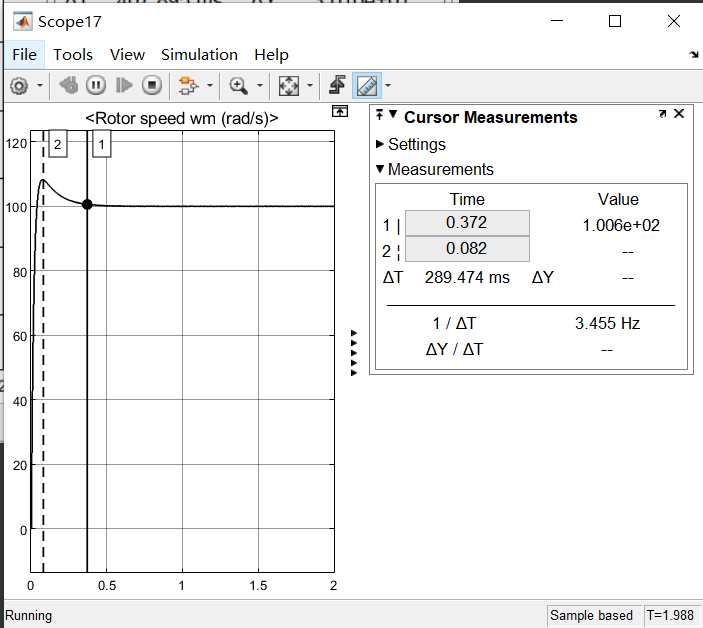
  • 参数测量：

    • 电流测量：实际电路设计中在电机驱动的桥上任意两相外接采样电阻获取电流参数，并根据基尔霍夫电流定率求取第三相电流值

    • 角度测量：实际中可以使用编码器获取电机运行角度，或使用无感FOC进行预测。

    • 仿真：通过测量模块导出即可

  • PI控制参数整定：

    KP=L2(Td+Ts)K_P=\frac{L}{2\left( T_d+T_s \right)}

    KI=R2(Td+Ts)K_I=\frac{R}{2\left( T_d+T_s \right)}

  • 已知逆变器开关周期为100us，设Td=0.5Ts=50us，代入武器站电机参数信息，可得：

    KP=L2(Td+Ts)=0.2K_P=\frac{L}{2\left( T_d+T_s \right)}=0.2

    KI=R2(Td+Ts)=100K_I=\frac{R}{2\left( T_d+T_s \right)}=100

  • 其电流输出波形如下所示【Id=0，Iq=10】：

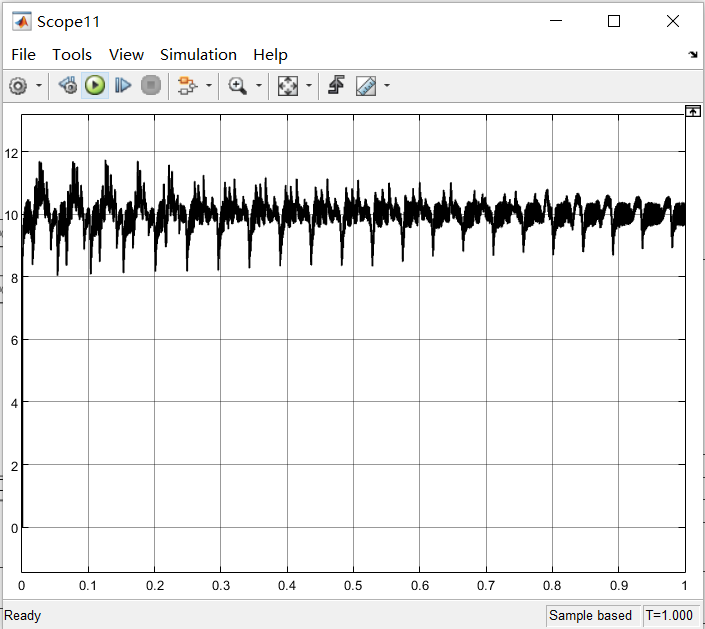
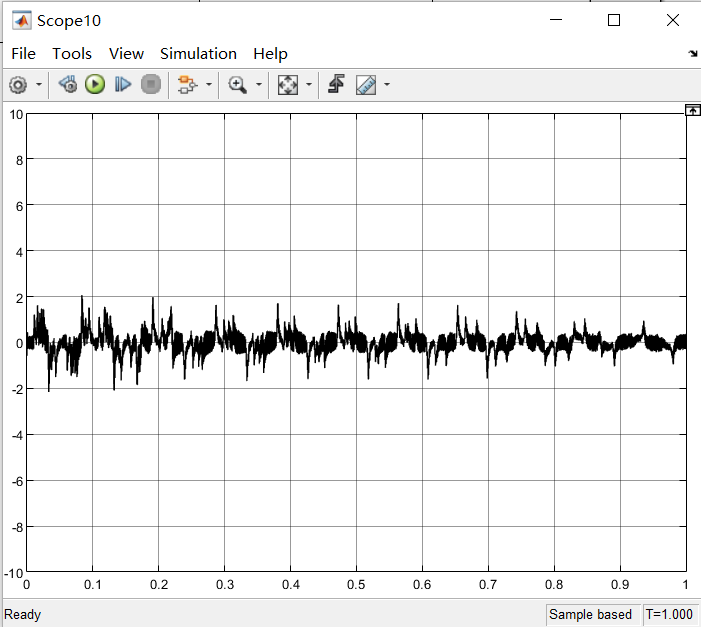
    1
    为什么会有噪声？因为在前面理论推导的时候忽略了电压方程中的耦合项的，但是在仿真过程中仍存在d-q两轴之间的耦合，因此输出波形存在高频噪声。

第三部分 Foc的PI速度环的仿真

  • 速度环作用：可以减少扰动对系统的影响、减小转速波动，使得系统工作在稳定的状态。

第一章 数学分析

  • 加入PI控制器消除极点后电流环开环传递函数为：

    G(s)=(KPL(Td+Ts)s2+s)=14(Td+Ts)2s2+2(Td+Ts)sG\left( s \right) =\left( \frac{\frac{K_P}{L}}{\left( T_d+T_s \right) s^2+s} \right) =\frac{1}{4\left( T_d+T_s \right) ^2s^2+2\left( T_d+T_s \right) s}

  • 由于采样时间很短，因此将其视为一个一型传递函数，可得电流环闭环传递函数为：

    G(s)=12(Td+Ts)s+1=13Tss+1G\left( s \right) =\frac{1}{2\left( T_d+T_s \right) s+1}=\frac{1}{3T_ss+1}

  • 忽略电机阻尼系数B，B=0

  • 速度环控制器存在一定的延时，因此加入一个一阶惯性系统，其Td=Ts

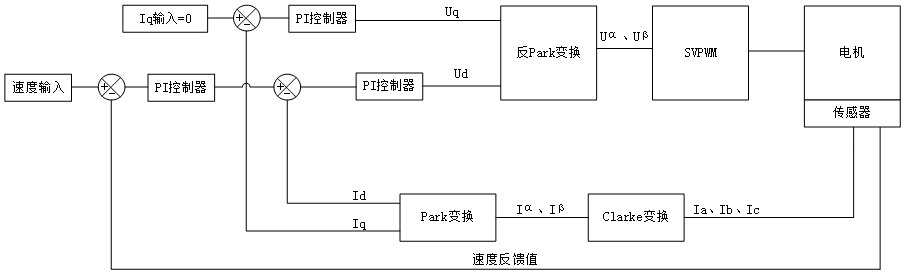
  • 速度环控制结构图：

  • 依据控制框图，可得速度环开环传递函数：

    G(s)=45PnψfKPπJKI⋅KIs+KPs2(3Ts2s2+4Tss+1)≈45PnψfKPπJ⋅KIs+KPs2KI(4Tss+1)G\left( s \right) =\frac{45P_n\psi _fK_P}{\pi JK_I}\cdot \frac{K_Is+K_P}{s^2\left( 3T_{s}^{2}s^2+4T_ss+1 \right)}\approx \frac{45P_n\psi _fK_P}{\pi J}\cdot \frac{K_Is+K_P}{s^2K_I\left( 4T_ss+1 \right)}

  • 简化表达式：

    τ=KIKP\tau =\frac{K_I}{K_P}

    代入可得：G(s)=45PnψfKPτπJ⋅τs+1s2(4Tss+1)代入可得： \\ G\left( s \right) =\frac{45P_n\psi _fK_P}{\tau \pi J}\cdot \frac{\tau s+1}{s^2\left( 4T_ss+1 \right)}

  • 设开环增益为1，$$\tau$$=0.01，使用matlab绘制bode图：

    1
    2
    Fun=tf([0.01 1],[0.0004 1 0 0])
    bode(Fun)

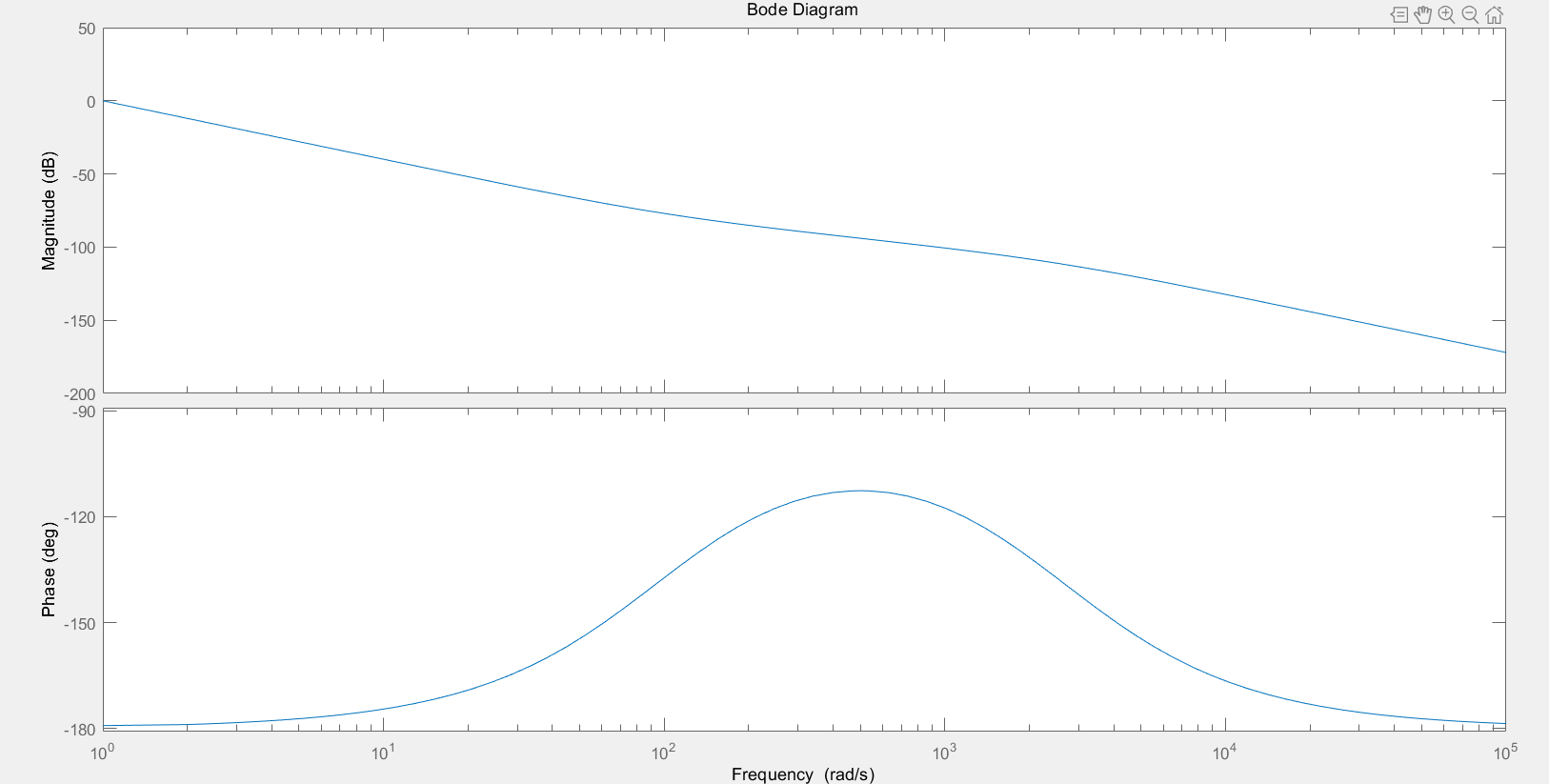
    image-20241031155046803

  • 分析Bode图：

    1. 有两个转折点，一个转折点频率是$$1/\tau$$，一个转折点频率是$$1/T_s$$

  • 自动控制原理：

    • 低频段特性由积分环节数和开环增益决定，其负斜率越大，位置越高则稳态性能越好。

      1. 斜率由积分环节个数决定，一个-20db
      2. 高度通过频率为1的时候，计算的幅值特性数值来衡量

    • 中频段反映了闭环系统动态响应的平稳性和快速性：

      • 相角裕度越小超调量越大，相角裕度越大超调量越小
      • 幅值穿越频率越小调节时间越大，穿越频率越大调节时间越小

    • 高频段反映了系统的抗干扰性能。

  • 依据Bode图设计控制系统：

    • 已知采样频率为100us，则转折频率2为2500，lg2500=3.39

    • 确定中频带宽值为2

    • 则可以计算出转折频率1，进而计算出$$\tau$$值

      τ=4Ts×10中频带宽值\tau =4T_s\times 10^{\text{中频带宽值}}

    • 为了减小超调量，因此我们需要尽量增大相角裕度，观察相频曲线，相角最大值位于中间，近似取幅值穿越频率为两个转折点的中点，进行计算可得：

      lg⁡wc=lg⁡14Ts−中频带宽2\lg w_c=\lg \frac{1}{4T_s}-\frac{\text{中频带宽}}{2}

    • 根据开环系数K的定义，可以计算出Kn的表达式：

      20lg⁡KN=40lg⁡1τ+20(lg⁡wc−lg⁡1τ)20\lg K_N=40\lg \frac{1}{\tau}+20\left( \lg w_c-\lg \frac{1}{\tau} \right)

    • 联立可得：

      {KN=45PnψfKPπJKI=1(4Ts)2101.5×中频带宽值τ=KIKP=4Ts×10中频带宽值\left\{ \begin{array}{l} K_N=\frac{45P_n\psi _fK_P}{\pi JK_I}=\frac{1}{\left( 4T_s \right) ^210^{1.5\times \text{中频带宽值}}}\\ \tau =\frac{K_I}{K_P}=4T_s\times 10^{\text{中频带宽值}}\\ \end{array} \right.

    • 求解计算PI控制器参数：

      {KP=πJ45×4×Ts×100.5×中频带宽值×Pn×ψfKI=πJ45×(4×Ts)2×101.5×中频带宽值×Pn×ψf\left\{ \begin{array}{l} K_P=\frac{\pi J}{45\times 4\times T_s\times 10^{0.5\times \text{中频带宽值}}\times P_n\times \psi _f}\\ K_I=\frac{\pi J}{45\times \left( 4\times T_s \right) ^2\times 10^{1.5\times \text{中频带宽值}}\times P_n\times \psi _f}\\ \end{array} \right.

    • 根据Matlab的PMSM电机模块参数，代入计算可得：

      1. 极对数：4
      2. 力矩常数：0.05 永磁体磁链：0.008333333
      3. 中频带宽：2
      4. Ts：100us
      5. 转动惯量：2.81e-4

      {KP=0.147KI=3.6782\left\{ \begin{array}{l} K_P=0.147\\ K_I=3.6782\\ \end{array} \right.

第二章 Simulink仿真

image-20241031172758003

  • KP = 0.147 KI=3.6782 速度给定值：100rad/s

  • 调整PI参数使其满足XXX驱动器协议性能要求：

    • Kp=0.3892 Ki=3.147

  • 综上，速度环仿真满足XXX驱动器协议要求：

    1. 驱动器电源：26±4V
    2. 电机最高转速：2000转/分
    3. 电机空载下转速变换率：≤0.5%
    4. 电机空载下转速响应时间：≤40ms
    5. 电机空载下超调量：≤8%

  1. 如何快速理解永磁同步电机？ - 知乎 (zhihu.com) ↩︎

  2. 保姆级电流环PI参数整定过程分析_带有交叉乘积项的电流pi环节-CSDN博客 ↩︎